3 Estruturas de Dados

Este segundo capítulo foi baseado no curso on-line Code School Try R e no livro Conhecendo o R: Um visão mais que estatística, modificações foram realizadas utilizando outros materiais que se encontram referenciados no final desse capítulo.

3.1 Vetor

Um vetor é simplesmente uma lista de valores. A maneira mais simples de usar um vetor é usando o comando c(), que concatena elementos num mesmo objeto. Exemplo:

x<- c(2,3,5,7,11) 
x

## [1]  2  3  5  7 11

Os argumentos de c() podem ser tanto elementos únicos quanto outros objetos. Adicione três números no vetor x:

y<- c(x,13,17,19)
y

## [1]  2  3  5  7 11 13 17 19

3.1.1 Vetores de Sequência

Se você precisar de um vetor com uma sequência de números, você pode criá-lo com a notação start:end. Vamos fazer um vetor com valores de 1 a 7:

1:7

## [1] 1 2 3 4 5 6 7

Uma maneira mais versátil de fazer sequências é chamar a função seq. Vamos fazer o mesmo com seq ():

seq(1:7)

## [1] 1 2 3 4 5 6 7

A função seq também permite que você use incrementos diferentes de 1. Experimente com as etapas de 0.5:

seq(1,7,0.5)

##  [1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0

seq(7,1,-0.5) 

##  [1] 7.0 6.5 6.0 5.5 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0

Todo objeto possui atributos intrínsecos, como tipo e tamanho. Com relação ao tipo, ele pode ser: numérico, caractere, complexo e lógico. Existem outros tipos, como por exemplo, funções ou expressões, porém esses não representam dados. As funções mode() e length() mostram o tipo e tamanho de um objeto, respectivamente:

z<-c(1,3,5,7,11) 
mode (z)

## [1] "numeric"

length(z)

## [1] 5

a <- "Angela"
b<-TRUE; 
c<-8i #objetos com tipos diferentes
mode(a); 

## [1] "character"

mode(b); 

## [1] "logical"

mode(c) #exibe os atributos "tipo" dos objetos 

## [1] "complex"

Se o vetor é muito longo e não “cabe” em uma linha, o R vai usar as linhas seguintes para continuar imprimindo o vetor:

longo<-100:50 #sequência decrescente de 100 a 50
longo #exibe o conteúdo do objeto 

##  [1] 100  99  98  97  96  95  94  93  92  91  90  89  88  87  86  85  84  83  82
## [20]  81  80  79  78  77  76  75  74  73  72  71  70  69  68  67  66  65  64  63
## [39]  62  61  60  59  58  57  56  55  54  53  52  51  50

Os números entre os colchetes não fazem parte do objeto e indicam a posição do vetor naquele ponto. Pode-se ver que [1] indica que o primeiro elemento do vetor estão naquela linha, e o [17] indica que a linha seguinte começa pelo décimo sétimo elemento do vetor e assim por diante.

Você pode recuperar um valor individual dentro de um vetor fornecendo seu índice numérico entre colchetes. Tente obter o valor 18:

longo[18]

## [1] 83

Muitas línguagens de programação iniciam índices de matriz em 0, mas os índices vetoriais de R começam em 1. Obtenha o primeiro valor digitando:

longo[1]

## [1] 100

Você pode atribuir novos valores dentro de um vetor existente. Tente mudar o terceiro valor 28:

longo [3] <- 28

Se você adicionar novos valores no final, o vetor aumentará para acomodá-los. Vamos adicionar um valor no final:

longo[101] <- 83

Você pode usar um vetor entre os colchetes para acessar vários valores. Tente obter a primeira e a terceira palavra:

longo[c(1,3)]

## [1] 100  28

Isso significa que você pode recuperar intervalos de valores. Obter a segunda e a quarta palavra:

longo[2:4]

## [1] 99 28 97

Você também pode definir intervalos de valores. Apenas fornecendo os valores em um vetor. Adicione valores 5 a 7:

longo[5:7] <- c(42,52,75)

Agora tente acessar o oitavo valor do vetor:

longo[8]

## [1] 93

3.1.2 Nomes de vetores

Para esse desafio, criaremos um vetor de 3 itens, e na sequência iremos armazená-lo na variável solo. Você pode atribuir nomes aos elementos de um vetor passando um segundo vetor preenchido com os nomes com a função names (), assim:

solo <- 1:3
names(solo) <- c("Argila", "Areia","Silte" )
solo

## Argila  Areia  Silte 
##      1      2      3

Agora defina o valor atual para o silte para um valor diferente usando o nome em vez da posição:

solo["Silte"]<-20

3.1.3 Plotando um vetor

A função barplot () desenha um gráfico de barras com os valores de um vetor. Vamos criar um novo vetor e armazená-lo na variável chuva.

Agora tente passar o vetor para a função barplot:

chuva <- c(20,50,85)
barplot(chuva)

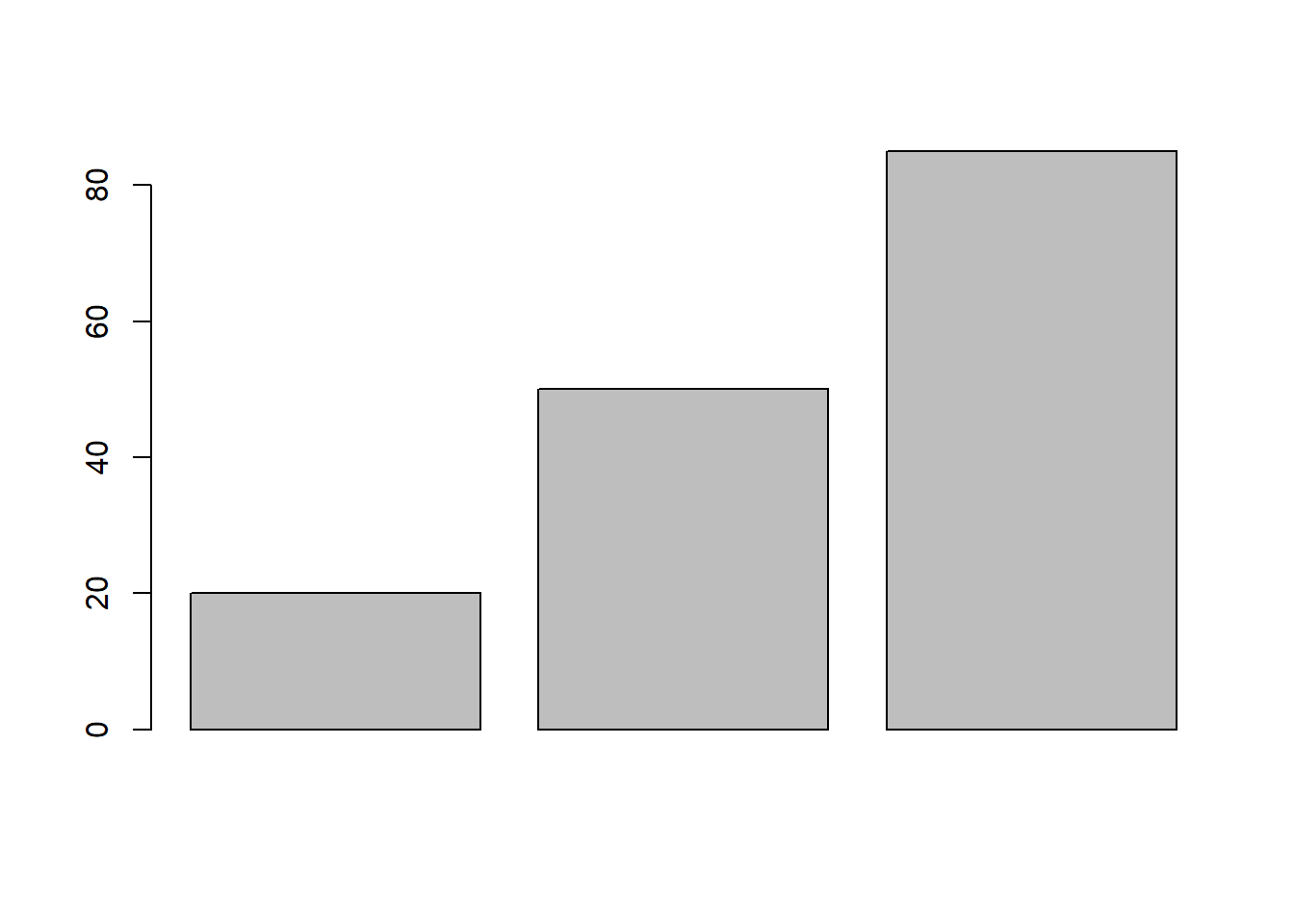
Se você atribuir nomes aos valores do vetor, o R usará esses nomes como rótulos no gráfico da barra. Vamos usar a função names () novamente:

names(chuva)<- c("Rondonópolis", "Maringá", "Cruzeiro do Sul")

Se você digitar barplot (chuva) com o vetor novamente, você verá os rótulos:

barplot(chuva)

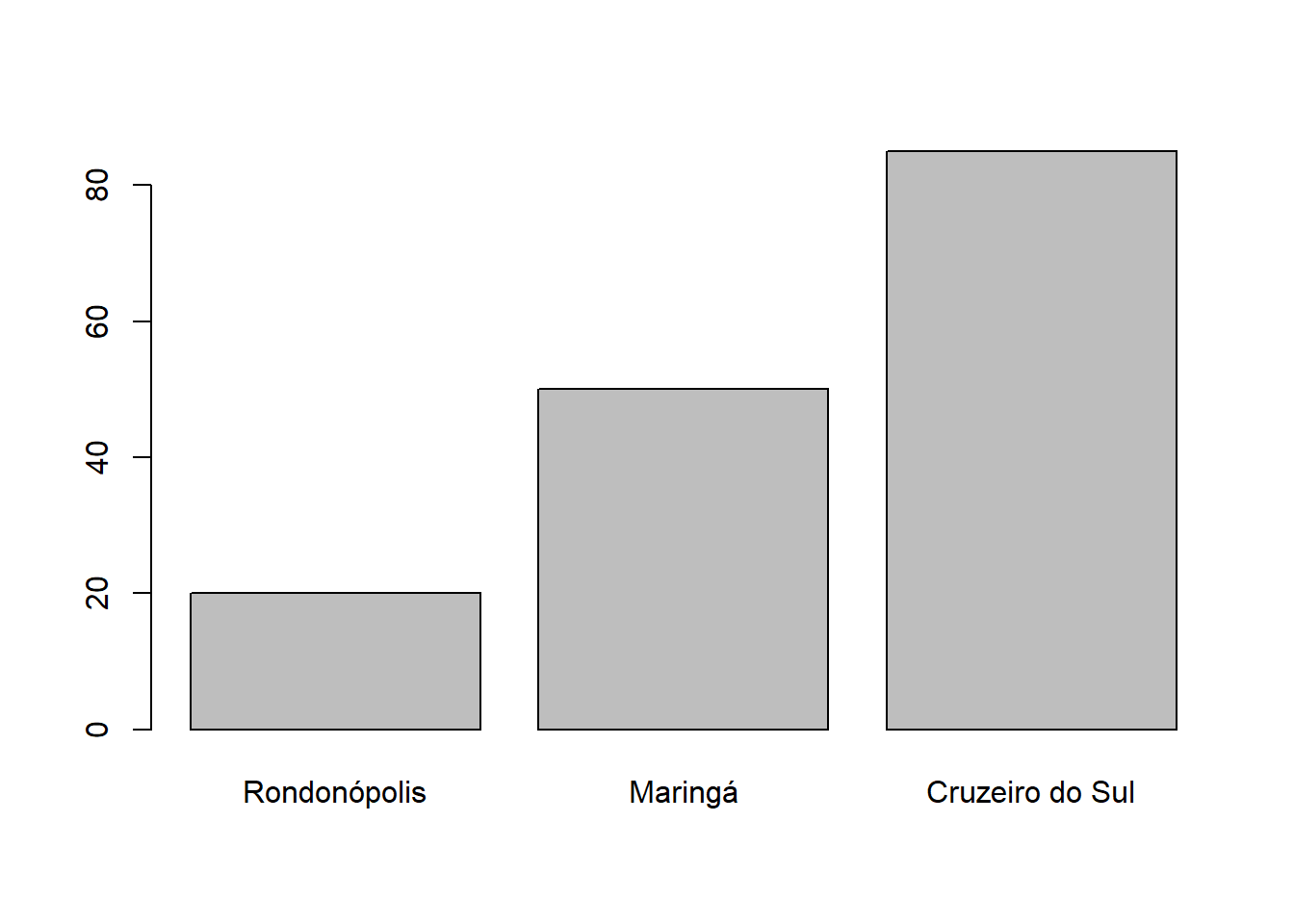
Tente chamar barplot em um vetor de números inteiros que variam de 1 a 100:

barplot(1:100)

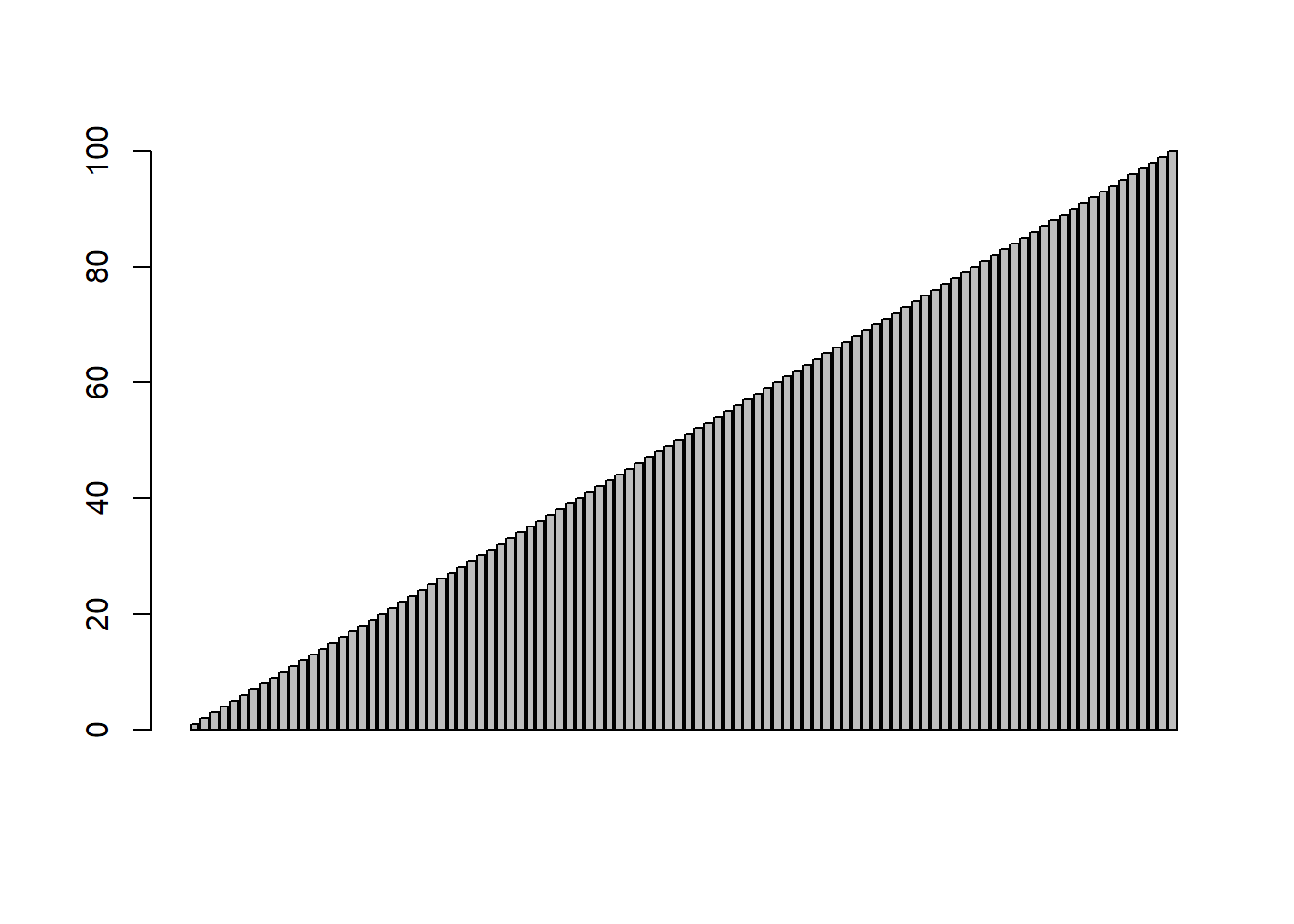
3.1.4 Operações matemáticas

A maioria das operações aritméticas funcionam tão bem em vetores quanto em valores únicos. Vamos fazer outro vetor de exemplo para você trabalhar e armazená-lo na variável a.

Se você adicionar um escalar (um único valor) a um vetor, o escalar será adicionado a cada valor no vetor, retornando um novo vetor com os resultados. Tente adicionar 1 a cada elemento em nosso vetor:

a <- c(1, 2, 3)
a + 1

## [1] 2 3 4

O mesmo se aplica na divisão, multiplicação ou qualquer outra aritmética básica. Tente dividir nosso vetor por 2:

a / 2

## [1] 0.5 1.0 1.5

Tente multiplicar nosso vetor por 2:

a*2

## [1] 2 4 6

Se você adicionar dois vetores, o R irá tirar cada valor de cada vetor e adicioná-los. Vamos fazer um segundo vetor para você experimentar e armazená-lo na variável b.

Tente adicioná-lo no vetor a:

b <- c(4,5,6)
a+b

## [1] 5 7 9

Agora tente subtrair b de a:

a-b

## [1] -3 -3 -3

Você também pode tirar dois vetores e comparar cada item. Veja quais valores nos vetores são iguais aos de um segundo vetor:

a == c(1, 99, 3)

## [1]  TRUE FALSE  TRUE

Observe que o R não testou se os vetores inteiros eram iguais, mas verificou cada valor no vetor a contar o valor no mesmo índice no nosso novo vetor.

Verifique se cada valor nos vetores são menores que o valor correspondente em outro vetor:

a < c(1, 99, 3)

## [1] FALSE  TRUE FALSE

Funções que normalmente funcionam com escalares também podem operar em cada elemento de um vetor. Tente obter o seno de cada valor em nosso vetor:

sin(a)

## [1] 0.8414710 0.9092974 0.1411200

Agora tente obter as raízes quadradas com a função sqrt:

sqrt(a)

## [1] 1.000000 1.414214 1.732051

3.1.5 Parcelas de dispersão

A função plot leva dois vetores, um para valores X e um para valores Y, e desenha um gráfico com eles.

Vamos desenhar um gráfico que mostre a relação de números e seus senos.

Primeiro, precisaremos de alguns dados de amostra. Criaremos um vetor com alguns valores fracionários entre 0 e 20, e iremos armazenó-lo na variável x. E na variável y um segundo vetor com os senos de x:

x <- seq(1, 20, 0.1)
y<-sin(x)

Em seguida basta chamar a função plot com seus dois vetores:

plot(x, y)

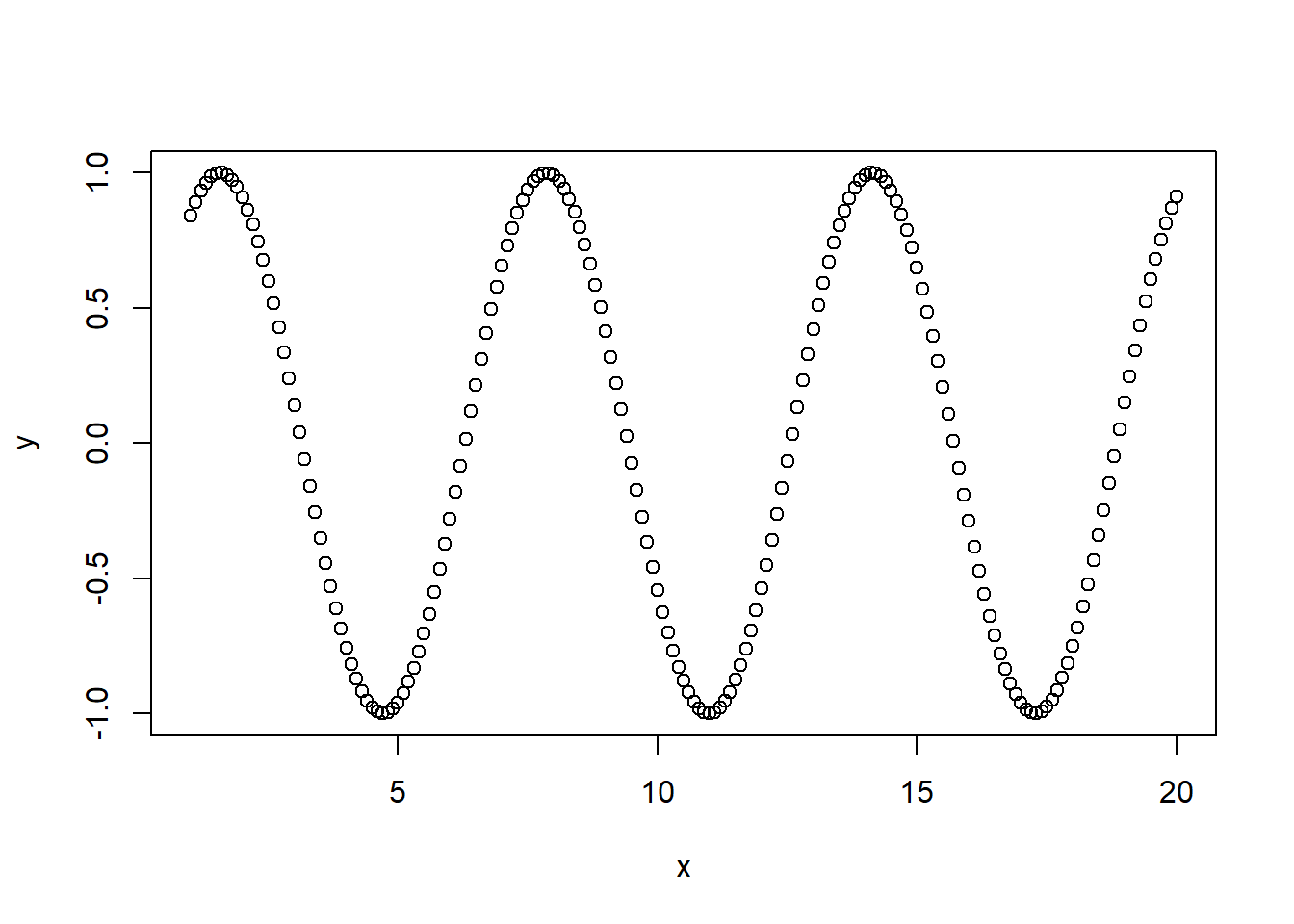
Observa-se sobre o gráfico que os valores do primeiro argumento (x) são usados para o eixo horizontal, e os valores do segundo (y) para o vertical.

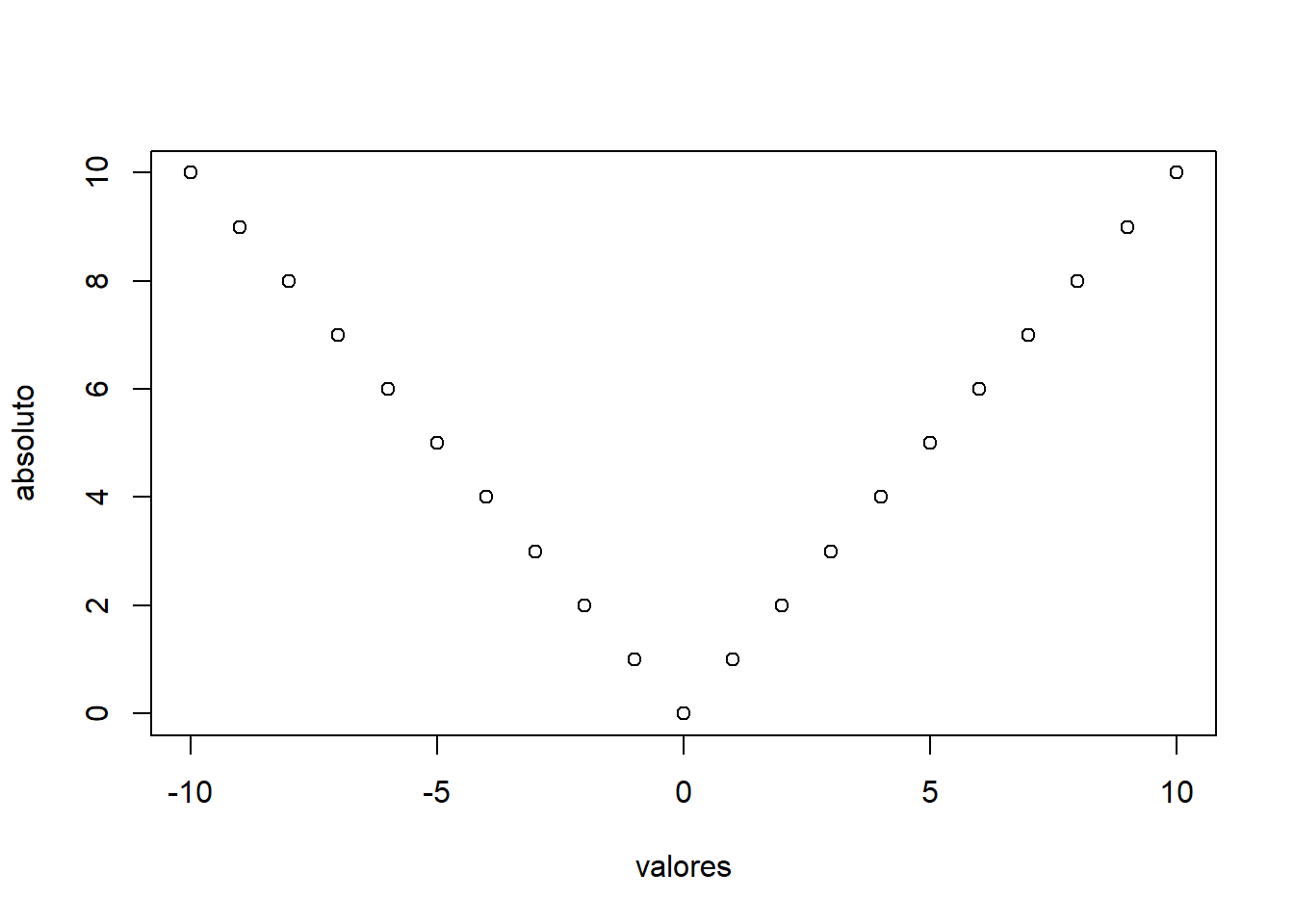
Vamos criar um vetor com alguns valores negativos e positivos e armazenó-lo na variável valores.

Também criaremos um segundo vetor com os valores absolutos do primeiro e armazenó-lo na variável absoluto.

Tente traçar os vetores, com os valores absolutos no eixo horizontal e no eixo vertical:

valores <- -10:10
absoluto<- abs(valores)
plot(valores, absoluto)

3.1.6 Valores Faltantes

Às vezes um determinado valor não está disponível ao trabalhar com dados de amostra. Mas não é uma boa idéia apenas tirar esses valores. O R tem um valor que indica explicitamente uma amostra que não estava disponível: NA. Muitas funções que funcionam com vetores tratam esses valor especialmente.

Vamos criar um vetor com uma amostra ausente e armazená-lo na variével a.

Tente obter a soma de seus valores e veja qual é o resultado:

a <- c(1, 3, NA, 7, 9)
sum(a)

## [1] NA

A soma é considerada “não disponível” por padrão porque um dos valores do vetor foi NA.

Lembre-se desse comando para mostrar ajuda para uma função. Apresente a ajuda para a função sum:

help(sum)

Como você vê na documentação, sum pode tomar um argumento opcional na.rm,. É configurado FALSE por padrão, mas se você configurá-lo com TRUE, todos os argumentos NA serão removidos do vetor antes do cálculo a ser executado.

Tente rondar sum novamente, com o na.rm conjunto para TRUE:

sum(a, na.rm = T)

## [1] 20

3.2 Matrizes

Há varias formas de criar uma matriz. O comando matriz() recebe um vetor como argumento e o transfoma em uma matrix de acordo com as dimensões. Vamos fazer uma matriz de 3 linhas de altura por 4 colunas de largura com todos os seus campos definidos em 0.

matrix(0,3,4)

##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0    0
## [2,]    0    0    0    0
## [3,]    0    0    0    0

Você também pode usar um vetor para inicializar o valor de uma matriz. Para preencher uma matriz de 3x4, você precisará de um vetor de 12 itens.

a <- (1:12)

print (a)

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

Agora chame a matrix com o vetor, o número de linhas e o número de colunas:

matrix (a,# chama o vetor
        3,# linha
        4) #coluna

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

Você também pode usar um vetor para inicializar o valor de uma matriz. Para preencher uma matriz 3x4, você precisará de um vetor de 12 itens:

a <-1:12
a

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

Agora chame a matrix com o vetor, o número de linhas e o número de colunas:

matrix (a,3,4)

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

3.2.1 Outras formas

matrix (a, 3)

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

Note que as matrizes são preenchidas ao longo das colunas. Para que a matriz seja preenchida por linhas deve-se alterar o argumento byrow, que por padrão está definido como FALSE, passe para TRUE:

matrix(a,3, byrow=T)

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

Os valores do vetor são copiados um por um para a nova matriz. Você também pode reformular o próprio vetor em uma matriz. Crie um vetor de 8 itens:

foliar <- 1:8

A função dim define as dimensões para uma matriz. Ele aceita um vetor com o número de linhas e o número de colunas a serem atribuídas. Atribua novas dimensões para foliar passando um vetor especificando 2 linhas e 4 colunas ( c(2, 4)):

dim(foliar) <- c(2,4)

O vetor não é mais unidimensional. Foi convertido no local para uma matriz. Agora, use a função matrix para criar uma matriz 5x5, com seus campos inicializados para qualquer valor que você desejar:

matrix (2,5,5)

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    2    2    2    2    2
## [2,]    2    2    2    2    2
## [3,]    2    2    2    2    2
## [4,]    2    2    2    2    2
## [5,]    2    2    2    2    2

3.2.2 Acesso a Matriz

Obter valores de matrizes não é diferente de vetores, você só precisa fornecer dois índices em vez de um. Abra a matriz foliar:

print (foliar)

##      [,1] [,2] [,3] [,4]
## [1,]    1    3    5    7
## [2,]    2    4    6    8

Tente obter o valor da segunda linha na terceira coluna da matriz foliar:

foliar[2,3]

## [1] 6

O valor da primeira linha da quarta coluna:

foliar[1,4]

## [1] 7

Você pode obter uma linha inteira da matriz omitindo o índice da coluna (mas mantenha a virgula). Tente recuperar a segunda linha:

foliar[2,]

## [1] 2 4 6 8

Para obter uma coluna inteira, omita o índice da linha. Recupere a quarta coluna:

foliar[,4]

## [1] 7 8

Você pode ler várias linhas ou colunas, fornecendo um vetor ou sequência com seus índices. Tente recuperar as colunas de 2 a 4:

foliar[,2:4]

##      [,1] [,2] [,3]
## [1,]    3    5    7
## [2,]    4    6    8

O comando summary pode ser usado para obter informações da matriz

summary(foliar)

##        V1             V2             V3             V4      
##  Min.   :1.00   Min.   :3.00   Min.   :5.00   Min.   :7.00  
##  1st Qu.:1.25   1st Qu.:3.25   1st Qu.:5.25   1st Qu.:7.25  
##  Median :1.50   Median :3.50   Median :5.50   Median :7.50  
##  Mean   :1.50   Mean   :3.50   Mean   :5.50   Mean   :7.50  
##  3rd Qu.:1.75   3rd Qu.:3.75   3rd Qu.:5.75   3rd Qu.:7.75  
##  Max.   :2.00   Max.   :4.00   Max.   :6.00   Max.   :8.00

Se desejar um resumo de todos os elementos da matriz, basta transformá-la em um vetor:

summary(as.vector(foliar))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    2.75    4.50    4.50    6.25    8.00

3.2.3 Visualizações em dados matriciais

Com um mapa de elevação. Tudo fica a 1 metro acima do nível do mar. Vamos criar uma matriz de 10 por 10 com todos os seus valores inicializados para 1:

elevacao <- matrix (1,10,10)

Na quarta linha, sexta coluna, defina a elevação para 0:

elevacao [4, 6] <- 0

Mapa de contorno dos valores passando a matriz para a função contour:

contour(elevacao)

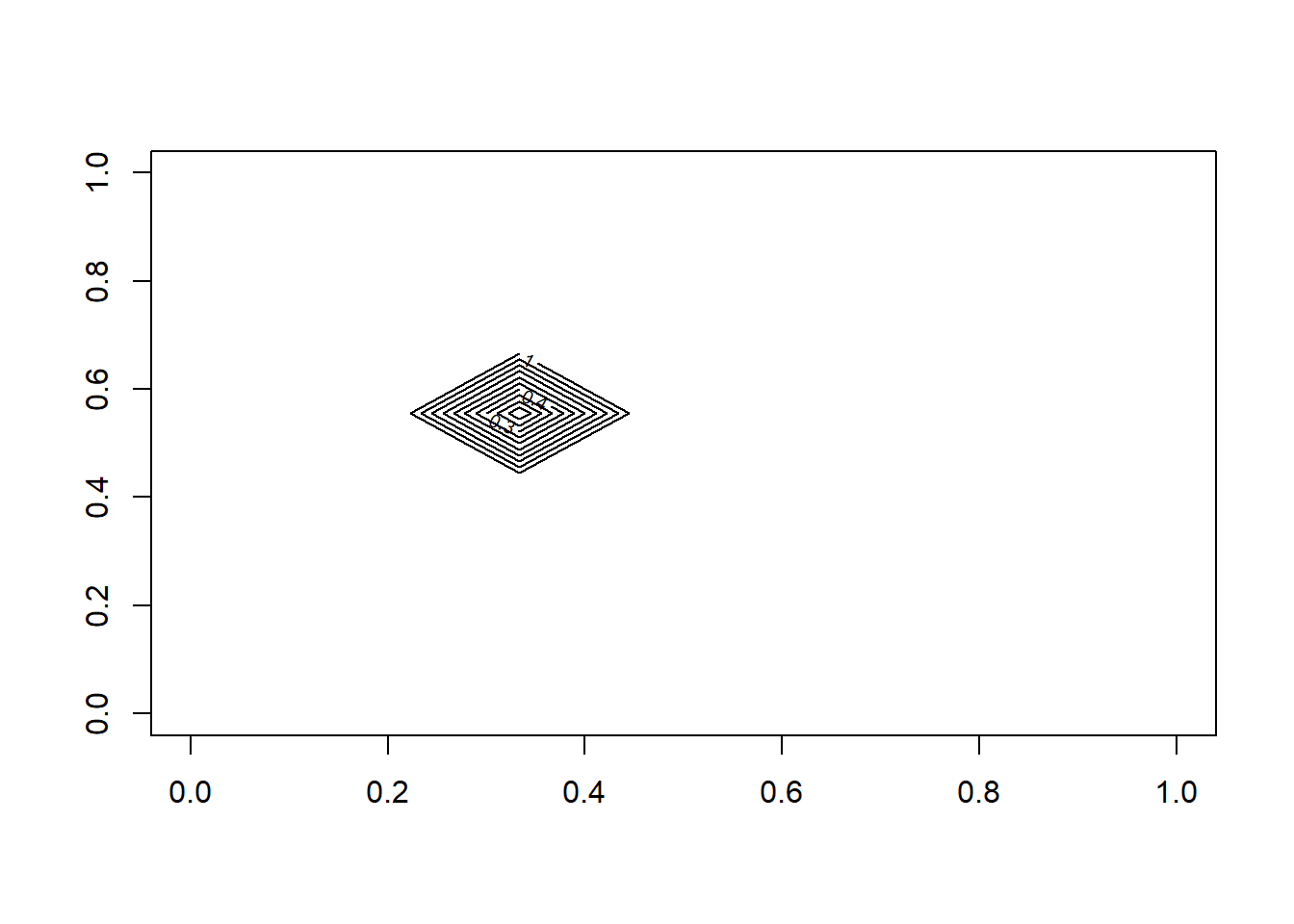
Criar um gráfico em perspectiva 3D com a função persp:

persp (elevacao)

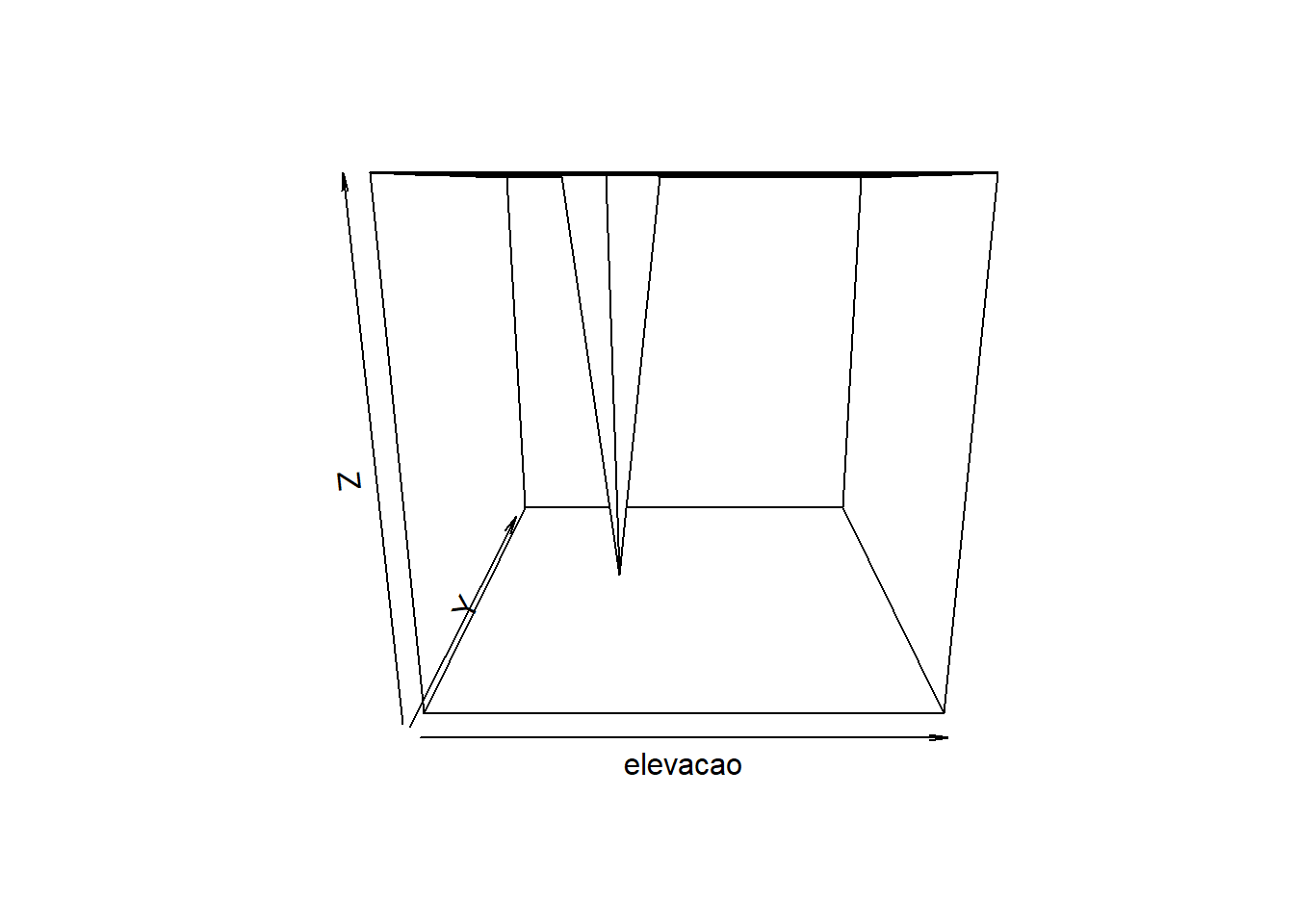
Podemos consertar isso especificando nosso próprio valor para o parâmetro expand:

persp (elevacao, expand =0.2)

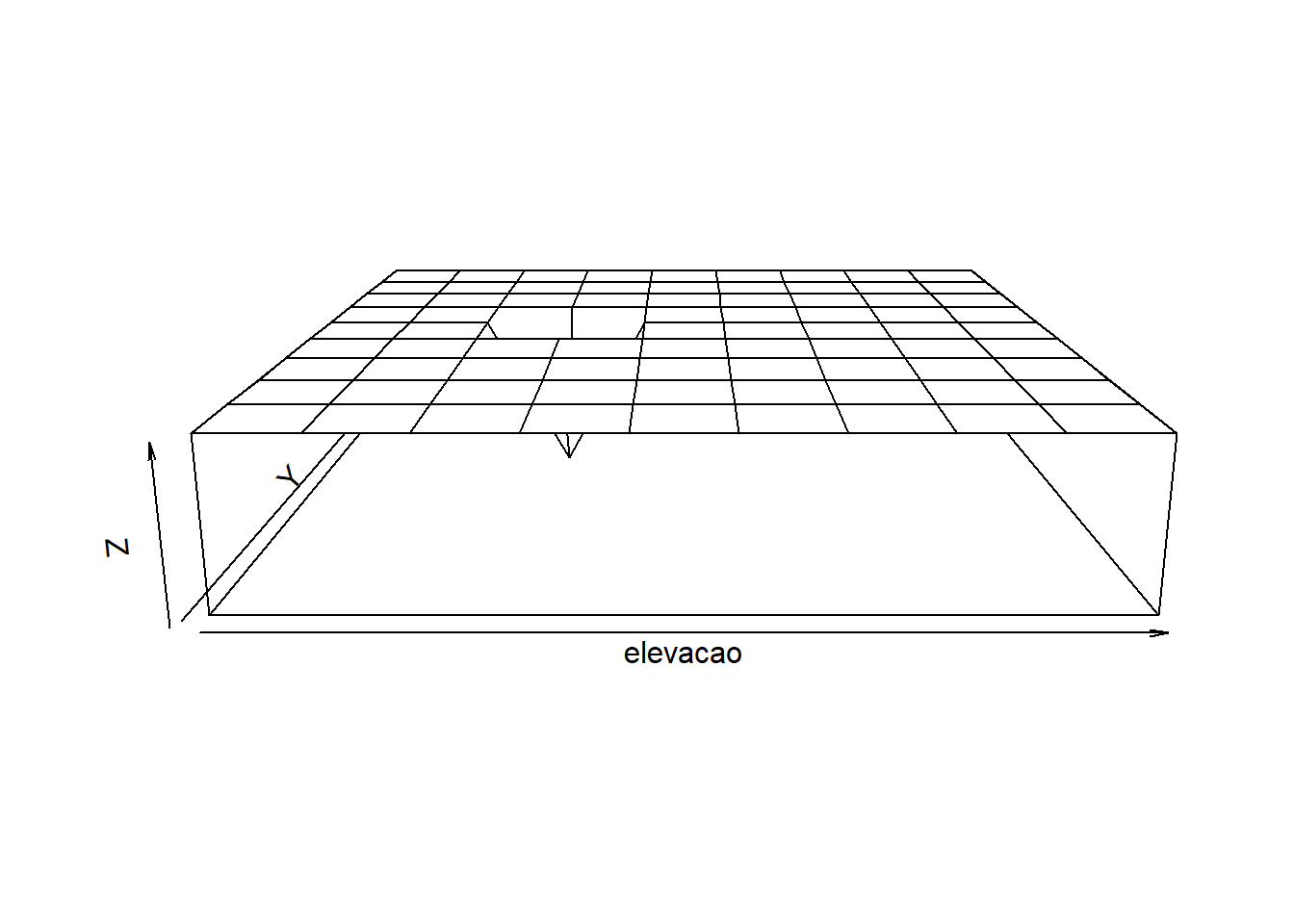
O R inclui alguns conjuntos de dados de amostra. Um deles é o volcanoum mapa 3D de um vulcão adormecido da Nova Zelândia.

É simplesmente uma matriz de 87x61 com valores de elevão, mas mostra o poder das visualizações de matriz do R. Criar um mapa de calor:

contour(volcano)

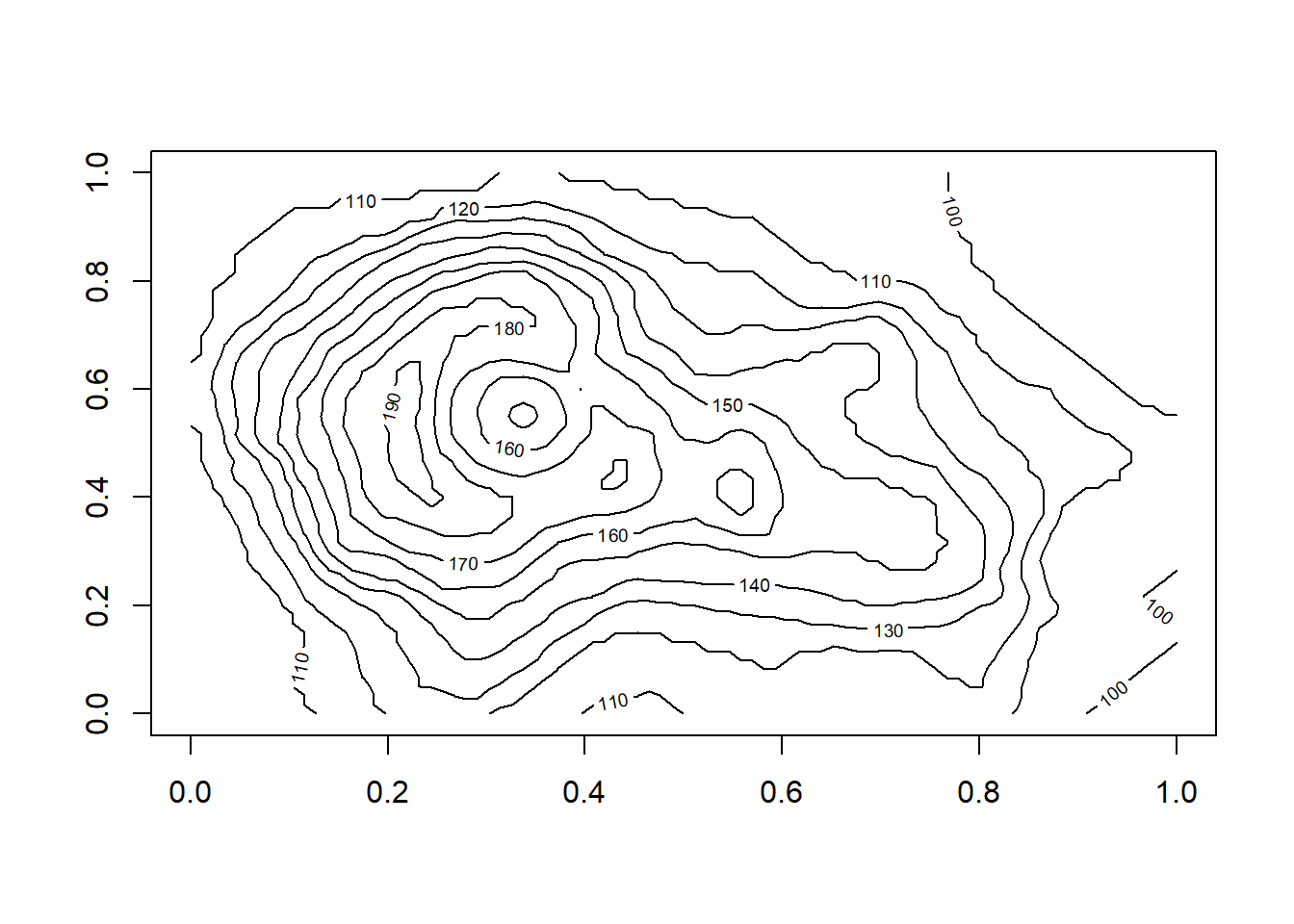
Gráfico em perspectiva:

persp(volcano, expand=0.2)

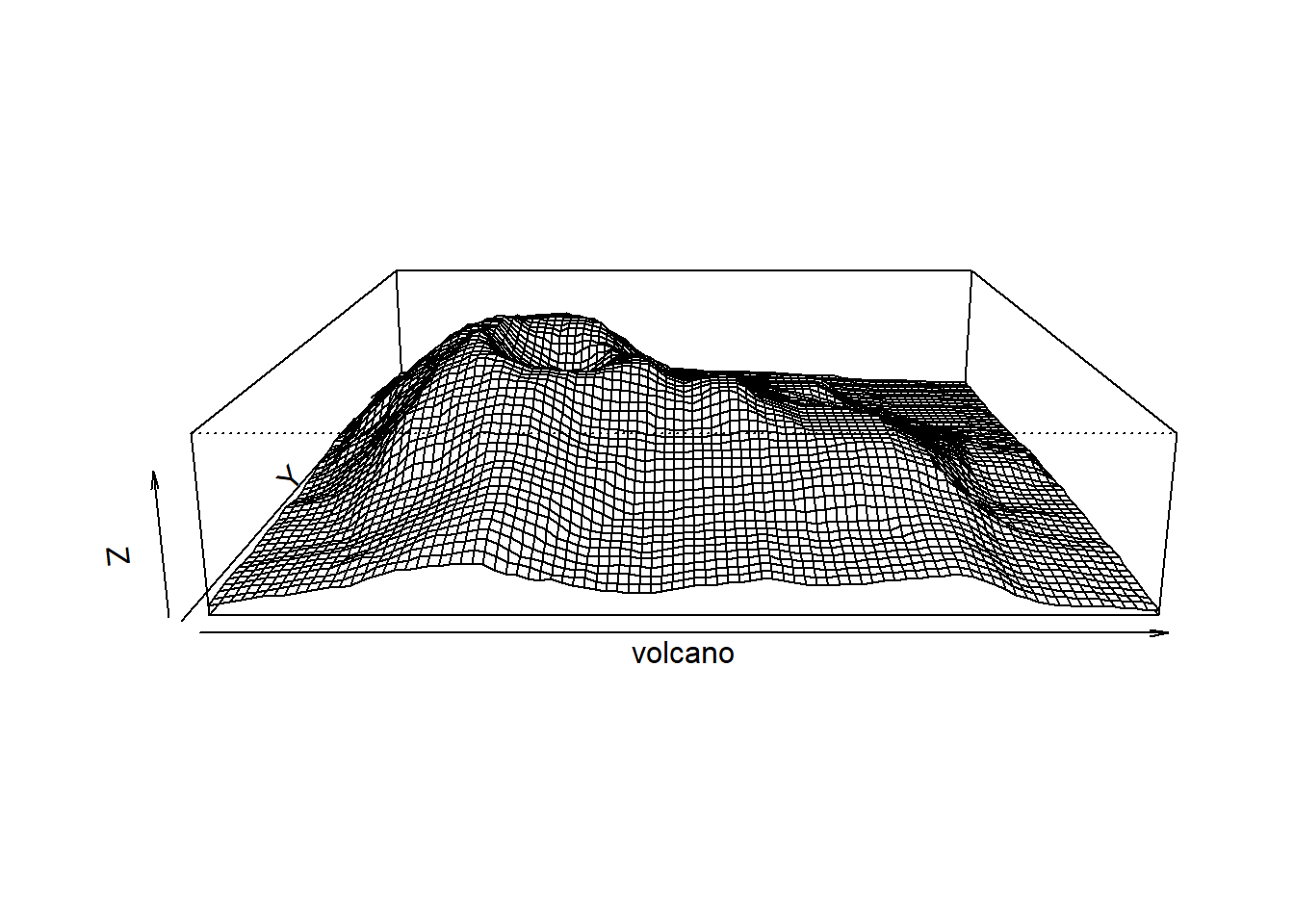
A função image cria um mapa de calor:

image(volcano)

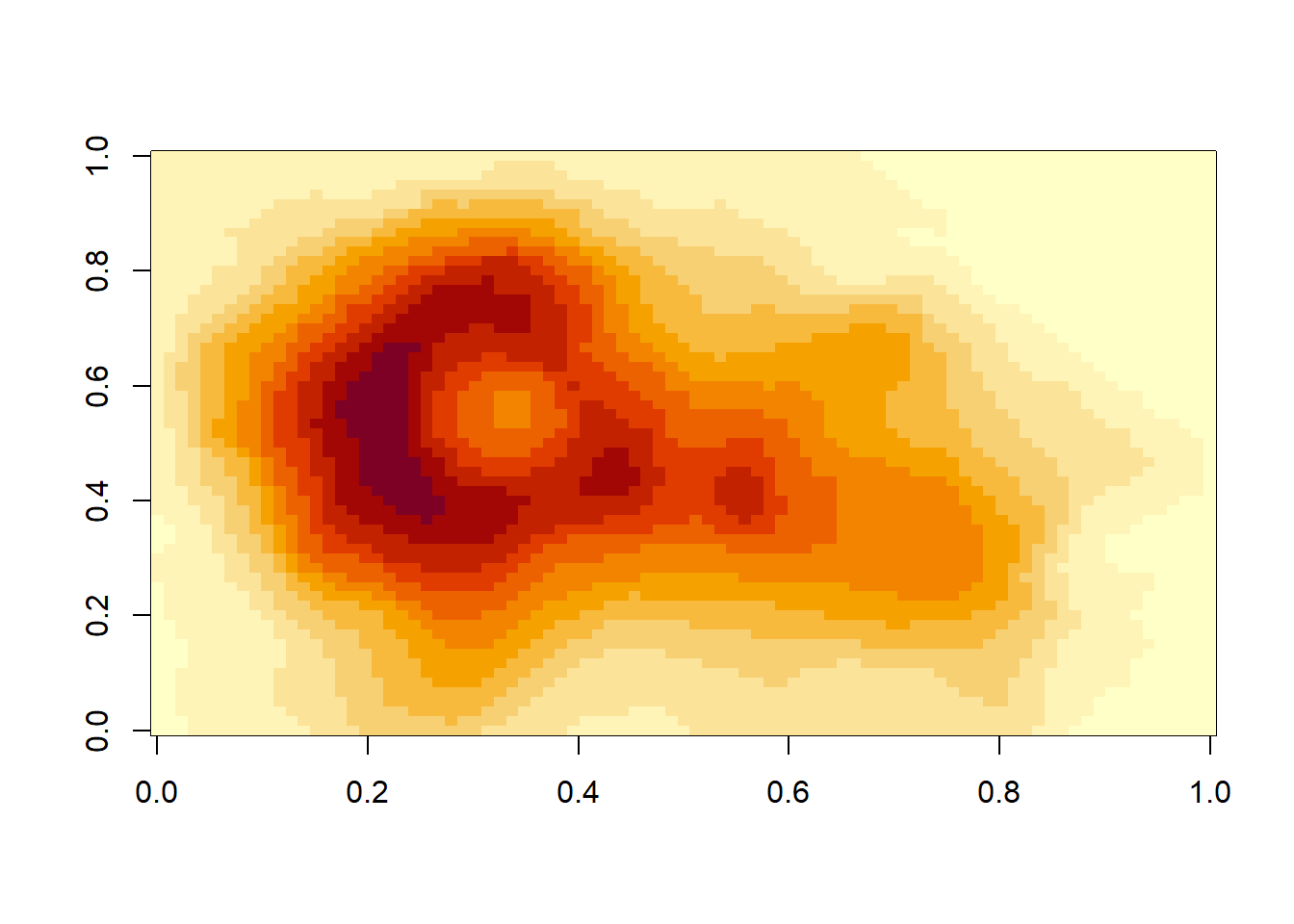
3.2.4 Mais informações sobre construções de Matrizes

Há outros comandos que podem ser usados para construir matrizes como cbind() e rbind (). Esses comandos concatenam colunas ou linhas, respectivamente na matriz (ou vetor):

a <- matrix (10:1,ncol=2) #construir uma matriz qualquer
a

##      [,1] [,2]
## [1,]   10    5
## [2,]    9    4
## [3,]    8    3
## [4,]    7    2
## [5,]    6    1

b <- cbind (a,1:5) #adicionar uma terceira coluna
b

##      [,1] [,2] [,3]
## [1,]   10    5    1
## [2,]    9    4    2
## [3,]    8    3    3
## [4,]    7    2    4
## [5,]    6    1    5

c<- rbind(b,c(28,28,28))
c

##      [,1] [,2] [,3]
## [1,]   10    5    1
## [2,]    9    4    2
## [3,]    8    3    3
## [4,]    7    2    4
## [5,]    6    1    5
## [6,]   28   28   28

Opcionalmente matrizes podem ter nomes associados às linhas e colunas (“rownames”e “colnames”). Cada um destes componentes da matrix é um vetor de nomes.

m1 <- matrix(1:12, ncol = 3) 

dimnames(m1) <- list(c("L1", "L2", "L3", "L4"), c("C1", "C2", "C3")) 
dimnames(m1)

## [[1]]
## [1] "L1" "L2" "L3" "L4"
## 
## [[2]]
## [1] "C1" "C2" "C3"

Matrizes são muitas vezes utilizadas para armazenar frequências de cruzamentos entre variáveis. Desta forma é comum surgir a necessidade de obter os totais marginais, isto é a soma dos elementos das linhas e/ou colunas das matrizes, o que pode ser diretamente obtido com margin.table( ):

 margin.table(m1, margin = 1)

## L1 L2 L3 L4 
## 15 18 21 24

 margin.table(m1, margin = 2)

## C1 C2 C3 
## 10 26 42

 apply(m1, 2, median)

##   C1   C2   C3 
##  2.5  6.5 10.5

3.3 Fatores

Os fatores são vetores em que os elementos pertencem a uma ou mais categorias temáticas. Por exemplo, ao criar um vetor de indicadores de “tratamentos” em uma análise de experimentos, devemos declarar este vetor como um “fator”. Pode criar um fator usando o comando factor(), ou o comando gl.

factor(rep(paste("T", 1:3, sep = ""), c(4, 4, 3)))

##  [1] T1 T1 T1 T1 T2 T2 T2 T2 T3 T3 T3
## Levels: T1 T2 T3

peso  <- c(134.8, 139.7, 147.6, 132.3, 161.7, 157.7, 150.3, 144.7,
           160.7, 172.7, 163.4, 161.3, 169.8, 168.2, 160.7, 161.0,
           165.7, 160.0, 158.2, 151.0, 171.8, 157.3, 150.4, 160.4,
           154.5, 160.4, 148.8, 154.0)
trat  <- rep(seq(0,300,50), each=4)  #?each
dados <-  data.frame(peso, trat=as.factor(trat))

3.4 Array

O conceito de array generaliza a idéia de matrix. Enquanto em uma matrix os elementos são organizados em duas dimensões (linhas e colunas), em um array os elementos podem ser organizados em um número arbitrário de dimensões. No R um array é definido utilizando a função array():

ar1 <- array(1:24, dim = c(3, 4, 2)) 
ar1

## , , 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12
## 
## , , 2
## 
##      [,1] [,2] [,3] [,4]
## [1,]   13   16   19   22
## [2,]   14   17   20   23
## [3,]   15   18   21   24

Veja agora um exemplo de dados já incluído no R no formato de array. Para “carregar” e visualizar os dados digite:

data(Titanic) 
Titanic

## , , Age = Child, Survived = No
## 
##       Sex
## Class  Male Female
##   1st     0      0
##   2nd     0      0
##   3rd    35     17
##   Crew    0      0
## 
## , , Age = Adult, Survived = No
## 
##       Sex
## Class  Male Female
##   1st   118      4
##   2nd   154     13
##   3rd   387     89
##   Crew  670      3
## 
## , , Age = Child, Survived = Yes
## 
##       Sex
## Class  Male Female
##   1st     5      1
##   2nd    11     13
##   3rd    13     14
##   Crew    0      0
## 
## , , Age = Adult, Survived = Yes
## 
##       Sex
## Class  Male Female
##   1st    57    140
##   2nd    14     80
##   3rd    75     76
##   Crew  192     20

Para obter maiores informações sobre estes dados digite: help(Titanic)

Agora vamos responder às seguintes perguntas, mostrando os comandos do R utilizados sobre o array de dados.

1. Quantas pessoas haviam no total?

sum(Titanic)

## [1] 2201

2. Quantas pessoas haviam na tripulação (crew)?

sum(Titanic[4, , , ])

## [1] 885

3. Quantas pessoas sobreviveram e quantas morreram?

apply(Titanic, 4, sum)

##   No  Yes 
## 1490  711

4. Quais as proporções de sobreviventes entre homens e mulheres?

margin.table(Titanic, margin = 1)

## Class
##  1st  2nd  3rd Crew 
##  325  285  706  885

margin.table(Titanic, margin = 2)

## Sex
##   Male Female 
##   1731    470

margin.table(Titanic, margin = 3)

## Age
## Child Adult 
##   109  2092

margin.table(Titanic, margin = 4)

## Survived
##   No  Yes 
## 1490  711

Esta função admite ainda índices múltiplos que permitem outros resumos da tabela de dados. Foi demonstrado como obter o total de sobreviventes e não sobreviventes, separados por sexo e depois as porcentagens de sobreviventes para cada sexo. Exemplo:

margin.table(Titanic, margin = c(2, 4))

##         Survived
## Sex        No  Yes
##   Male   1364  367
##   Female  126  344

prop.table(margin.table(Titanic, margin = c(2, 4)), margin = 1)

##         Survived
## Sex             No       Yes
##   Male   0.7879838 0.2120162
##   Female 0.2680851 0.7319149

prop.table(margin.table(Titanic, margin = c(2, 1)), margin = 1)

##         Class
## Sex             1st        2nd        3rd       Crew
##   Male   0.10398614 0.10340843 0.29462738 0.49797805
##   Female 0.30851064 0.22553191 0.41702128 0.04893617

3.5 Data.frame

Os datas.frames são muito semelhantes quando comparados às matrizes, pois têm linhas e colunas, portanto duas dimensões. Entretando, diferentemente das matrizes, colunas diferentes podem armazenar elementos de tipos diferentes. Por exemplo, a primeira coluna pode ser numérica, enquanto a segunda constituida de caracteres. Cada coluna precisa ter o mesmo tamanho. Criar o vetor nomes:

nome <- c("Melissa José",
          "Jennifer Linhares",
          "Gedilene Ponciano",
          "Edinar da Silva",
          "Osmar Emidio",
          "Jeeziel Vieira")

Criar vetor idade:

idade <- c(17,18,16,15,15,18)

Criar vetor sexo (categoria=fator):

sexo <- factor(c("F","F","F","F","M","M"))

Criar vetor altura:

alt <- c(180,170,160,150,140,168)

Reunir tudo em um data.frame:

dados <- data.frame(nome, idade, sexo, alt)

Ver atributos da tabela:

str(dados)

## 'data.frame':    6 obs. of  4 variables:
##  $ nome : Factor w/ 6 levels "Edinar da Silva",..: 5 4 2 1 6 3
##  $ idade: num  17 18 16 15 15 18
##  $ sexo : Factor w/ 2 levels "F","M": 1 1 1 1 2 2
##  $ alt  : num  180 170 160 150 140 168

Adicionar nome às linhas com o comando row.names():

row.names(dados) <- c(1,2,3,4,5,6)
dados

##                nome idade sexo alt
## 1      Melissa José    17    F 180
## 2 Jennifer Linhares    18    F 170
## 3 Gedilene Ponciano    16    F 160
## 4   Edinar da Silva    15    F 150
## 5      Osmar Emidio    15    M 140
## 6    Jeeziel Vieira    18    M 168

names(dados) <- c("Nome", "Idade", "Sexo", "altura")
dados

##                Nome Idade Sexo altura
## 1      Melissa José    17    F    180
## 2 Jennifer Linhares    18    F    170
## 3 Gedilene Ponciano    16    F    160
## 4   Edinar da Silva    15    F    150
## 5      Osmar Emidio    15    M    140
## 6    Jeeziel Vieira    18    M    168

3.5.1 Índice dos Data.frames

Buscar elementos:

dados[2,1] #elemento da  linha  2, coluna 1

## [1] Jennifer Linhares
## 6 Levels: Edinar da Silva Gedilene Ponciano ... Osmar Emidio

dados[2,] #toda linha dois

##                Nome Idade Sexo altura
## 2 Jennifer Linhares    18    F    170

Repare que apesar de “Nomes” ter sido criado como vetor de caracteres, o R passou a entender como um fator dentro do data.frame:

dados[,1]

## [1] Melissa José      Jennifer Linhares Gedilene Ponciano Edinar da Silva  
## [5] Osmar Emidio      Jeeziel Vieira   
## 6 Levels: Edinar da Silva Gedilene Ponciano ... Osmar Emidio

Transformar para caracteres:

dados[,1] <- as.character(dados[,1])
dados[,1]

## [1] "Melissa José"      "Jennifer Linhares" "Gedilene Ponciano"
## [4] "Edinar da Silva"   "Osmar Emidio"      "Jeeziel Vieira"

Acessando os dados:

dados$Nome

## [1] "Melissa José"      "Jennifer Linhares" "Gedilene Ponciano"
## [4] "Edinar da Silva"   "Osmar Emidio"      "Jeeziel Vieira"

dados$Nome[3]

## [1] "Gedilene Ponciano"

dados$Nome [1:3]

## [1] "Melissa José"      "Jennifer Linhares" "Gedilene Ponciano"

str(dados)

## 'data.frame':    6 obs. of  4 variables:
##  $ Nome  : chr  "Melissa José" "Jennifer Linhares" "Gedilene Ponciano" "Edinar da Silva" ...
##  $ Idade : num  17 18 16 15 15 18
##  $ Sexo  : Factor w/ 2 levels "F","M": 1 1 1 1 2 2
##  $ altura: num  180 170 160 150 140 168

3.5.2 Manipulando um Data.frame

Você pode manipular um data.frame adicionando ou eliminando colunas ou linhas, assim como em matrizes. Pode-se usar os comandos cbind() e rbind () para adcionar colunas e linhas respectivamente a um data.frame:

dados <- cbind (dados, #adicionar uma coluna
               Conceito=c("A","A","A","C","A","B"))

dados <- rbind (dados, #adicionar uma linha
                "7"= c("Caio Pinto", 21, "M", 172, "C"))
dados

##                Nome Idade Sexo altura Conceito
## 1      Melissa José    17    F    180        A
## 2 Jennifer Linhares    18    F    170        A
## 3 Gedilene Ponciano    16    F    160        A
## 4   Edinar da Silva    15    F    150        C
## 5      Osmar Emidio    15    M    140        A
## 6    Jeeziel Vieira    18    M    168        B
## 7        Caio Pinto    21    M    172        C

Assim como para vetores e matrizes, você pode selecionar um subgrupo de um data.frame e armazená-lo em um outro objeto ou utilizar índices como o sinal negativo para eliminar linhas ou colunas de um data.frame:

dados<- dados [1:6,] #selecionar linha de 1 a 6
dados<- dados [,-5] #excluir a quinta coluna
dados

##                Nome Idade Sexo altura
## 1      Melissa José    17    F    180
## 2 Jennifer Linhares    18    F    170
## 3 Gedilene Ponciano    16    F    160
## 4   Edinar da Silva    15    F    150
## 5      Osmar Emidio    15    M    140
## 6    Jeeziel Vieira    18    M    168

dados[dados$Sexo=="F",] #exibir só masculinos

##                Nome Idade Sexo altura
## 1      Melissa José    17    F    180
## 2 Jennifer Linhares    18    F    170
## 3 Gedilene Ponciano    16    F    160
## 4   Edinar da Silva    15    F    150

A ordenação das linhas de um data.frame segundo os dados contidos em determinadas colunas também é extremamente útil:

dados [order(dados$altura),]

##                Nome Idade Sexo altura
## 5      Osmar Emidio    15    M    140
## 4   Edinar da Silva    15    F    150
## 3 Gedilene Ponciano    16    F    160
## 6    Jeeziel Vieira    18    M    168
## 2 Jennifer Linhares    18    F    170
## 1      Melissa José    17    F    180

dados [rev(order(dados$altura)),]

##                Nome Idade Sexo altura
## 1      Melissa José    17    F    180
## 2 Jennifer Linhares    18    F    170
## 6    Jeeziel Vieira    18    M    168
## 3 Gedilene Ponciano    16    F    160
## 4   Edinar da Silva    15    F    150
## 5      Osmar Emidio    15    M    140

3.5.3 Separando um data.frame por grupos

split (dados, sexo)

## $F
##                Nome Idade Sexo altura
## 1      Melissa José    17    F    180
## 2 Jennifer Linhares    18    F    170
## 3 Gedilene Ponciano    16    F    160
## 4   Edinar da Silva    15    F    150
## 
## $M
##             Nome Idade Sexo altura
## 5   Osmar Emidio    15    M    140
## 6 Jeeziel Vieira    18    M    168

3.6 Lista

Listas são objetos muito úteis, pois são usadas para combinar diferentes estruturas de dados em um mesmo objeto, ou seja, vetores, matrizes, arrays, data.frames e até mesmo outras listas:

pes <- list (idade=32, nome="Maria", notas=c(98,95,78), B=matrix(1:4,2,2))
pes

## $idade
## [1] 32
## 
## $nome
## [1] "Maria"
## 
## $notas
## [1] 98 95 78
## 
## $B
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

Listas são construídas com o comando list (). Quando você exibe um objeto que é uma lista, cada componente é exibido com o seu nome $ ou [ ]:

3.6.1 Alguns comandos que retornam listas

Muitos comandos do R retornam seu resultado na forma de listas. Um exemplo pode ser visualizado com o uso do comando t.tes(), que retorna um objeto, sendo este uma lista:

x <- c(1,3,2,3,4)
y <- c(4,5,5,4,4)
tt <- t.test (x,y, var.equal=T)
tt

## 
##  Two Sample t-test
## 
## data:  x and y
## t = -3.182, df = 8, p-value = 0.01296
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -3.1044729 -0.4955271
## sample estimates:
## mean of x mean of y 
##       2.6       4.4

Comprovar que é uma lista:

is.list(tt)

## [1] TRUE

mode (tt)

## [1] "list"

Exibir o componentes da lista:

names(tt)

##  [1] "statistic"   "parameter"   "p.value"     "conf.int"    "estimate"   
##  [6] "null.value"  "stderr"      "alternative" "method"      "data.name"

tt$conf.int #intervalo de confianca 

## [1] -3.1044729 -0.4955271
## attr(,"conf.level")
## [1] 0.95

3.7 Referência

MELO, M. P.; PETERNELI, L. A. Conhecendo o R: Um visão mais que estatística. Viçosa, MG: UFV, 2013. 222p.

Prof. Paulo Justiniando Ribeiro >http://www.leg.ufpr.br/~paulojus/<

Prof. Adriano Azevedo Filho >http://rpubs.com/adriano/esalq2012inicial<

Prof. Fernando de Pol Mayer >https://fernandomayer.github.io/ce083-2016-2/<

Site Interativo Datacamp >https://www.datacamp.com/<