8 Analise de variância (ANOVA)

Estudos estatísticos contemporâneos contemplam a análise de variância tendo em vista que este procedimento permite identificar e quantificar as variações ocorridas em um experimento, discriminando a parte da variação associada ao modelo pelo qual o experimento foi procedido da variação que se dá devido ao acaso. No R encontram-se diversos procedimentos para se executar a ANOVA. A tabela abaixo mostra alguns modelos e suas usuais formulações:

Modelo	Fórmula	Comentário
DIC	y~t	t é um fator
DBC	y~t+b	t e b são fatores
DQL	y~t+l+c	t, l e c são fatores
Fatorial/ DIC	y~N*P	igual a N + P + N:P
Fatorial/ DBC	y~b+N*P	igual a b+N+P+N:P
Regressão linear simples	y~x	x é uma variável exploratória
Regressão quadrática	y~x+x2	x2 é um objeto x2<-x^2

Os modelos de análise de variância simples podem ser trabalhados também a partir da função lm() simplesmente indicando um fator como variável independente. No entanto, existem outras funções que também realizam análises de variância para casos específicos (como a aov() para amostras balanceadas) ou modelos lineares mais complexos como análise de modelos mistos ou hierarquicas função lme() do pacote nlme e modelos não lineares nls() e glm() para ANOVA, com estrutura de erros especificada.

8.1 Delineamento inteiramente casualizado

O delineamento inteiramente casualizado é o mais simples de todos os delineamentos experimentais.

Este delineamento apresenta as seguintes caracterítiscas:

Utiliza apenas os princópios da repetição e da casualização, deixando de lado o princípio do controle local, e, portanto, as repetições não são organizadas em blocos;
Os tratamentos são designados às parcelas de forma inteiramente casual, com números iguais ou diferentes repetições por tratamento.

Vantagens em relações a outros delineamentos

é um delineamento bastante flexível, visto que o número de tratamentos e de repetições depende apenas do número de parcelas disponíveis;
o número de repetições pode ser diferente de um tratamento para outro;
a análise estatística é simples, mesmo quando o número de repetições por tratamento é variável;
o número de grau de liberdade para o resíduo é o maior possível;

Desvantagens em relações a outros delineamentos

exige homogeneidade total das condições experimentais;
pode conduzir a uma estimativa de variância residual bastante alta, uma vez que, não se aplica o controle local;

Este delineamento é mais utilizado em experimentos de laboratório e nos ensaios com vasos, realizados dentro de casas de vegetação, nos quais as condições experimentais podem ser controladas. Nos experimentos realizados com vasos, estes devem ser cte mudados de posição, de forma interamente casual.

8.1.1 Análise de experimento em DIC

Dados de um experimento visando controle de pulgão (Aphis gossypii Glover) em cultura de pepino, instalado em delineamento inteiramente casualizado com 6 repetições. A resposta observada foi o número de pulgões após a aplicação de produtos indicados para seu controle. O primeiro passo é ler os dados.

Importando dados:

dados <- read.table("https://www.dropbox.com/s/jjyo8dhyy0qt3ft/BanzattoQd3.2.1.txt?dl=1")

Conferir se temos fatores para fazer a análise de variância:

str(dados)

## 'data.frame':    30 obs. of  3 variables:
##  $ trat   : Factor w/ 5 levels "Azinfos etilico",..: 5 1 3 4 2 5 1 3 4 2 ...
##  $ rept   : int  1 1 1 1 1 2 2 2 2 2 ...
##  $ pulgoes: int  2370 1282 562 173 193 1687 1527 321 127 71 ...

Lembramos que pulgões deve ter conteúdo numérico e trat deve ser fator:

dados$trat<-as.factor(dados$trat)
dados$pulgoes<-as.numeric(dados$pulgoes)

Verificação gráfica** É importante notar que as barras simplesmente refletem a variância dos dados dentro de cada tratamento e não são adequadas para detectar diferenças entre tratamentos:

plot(dados$trat, dados$pulgoes)

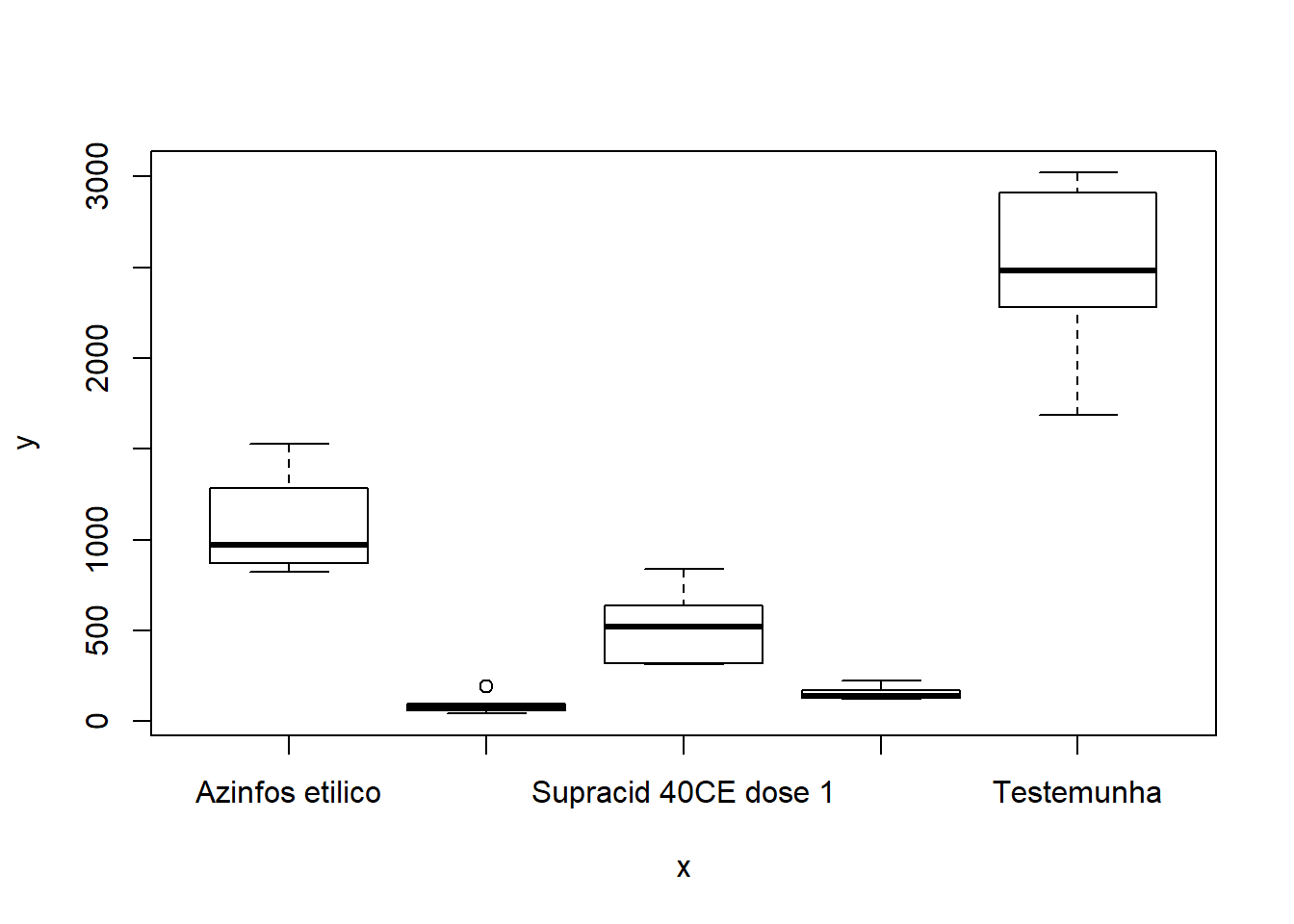
8.1.2 Análise de variância

Fazendo a análise de variância:

m0 <- lm (dados$pulgoes ~ dados$trat)

anova(m0)

## Analysis of Variance Table
## 
## Response: dados$pulgoes
##            Df   Sum Sq Mean Sq F value    Pr(>F)    
## dados$trat  4 23145259 5786315   81.79 5.505e-14 ***
## Residuals  25  1768644   70746                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Extraindo o coeficiênte de variação:

require(agricolae)

## Loading required package: agricolae

cv.model(m0)

## [1] 30.73619

Análise gráfica dos resíduos:

par(mfrow = c(2,2))
plot(m0)

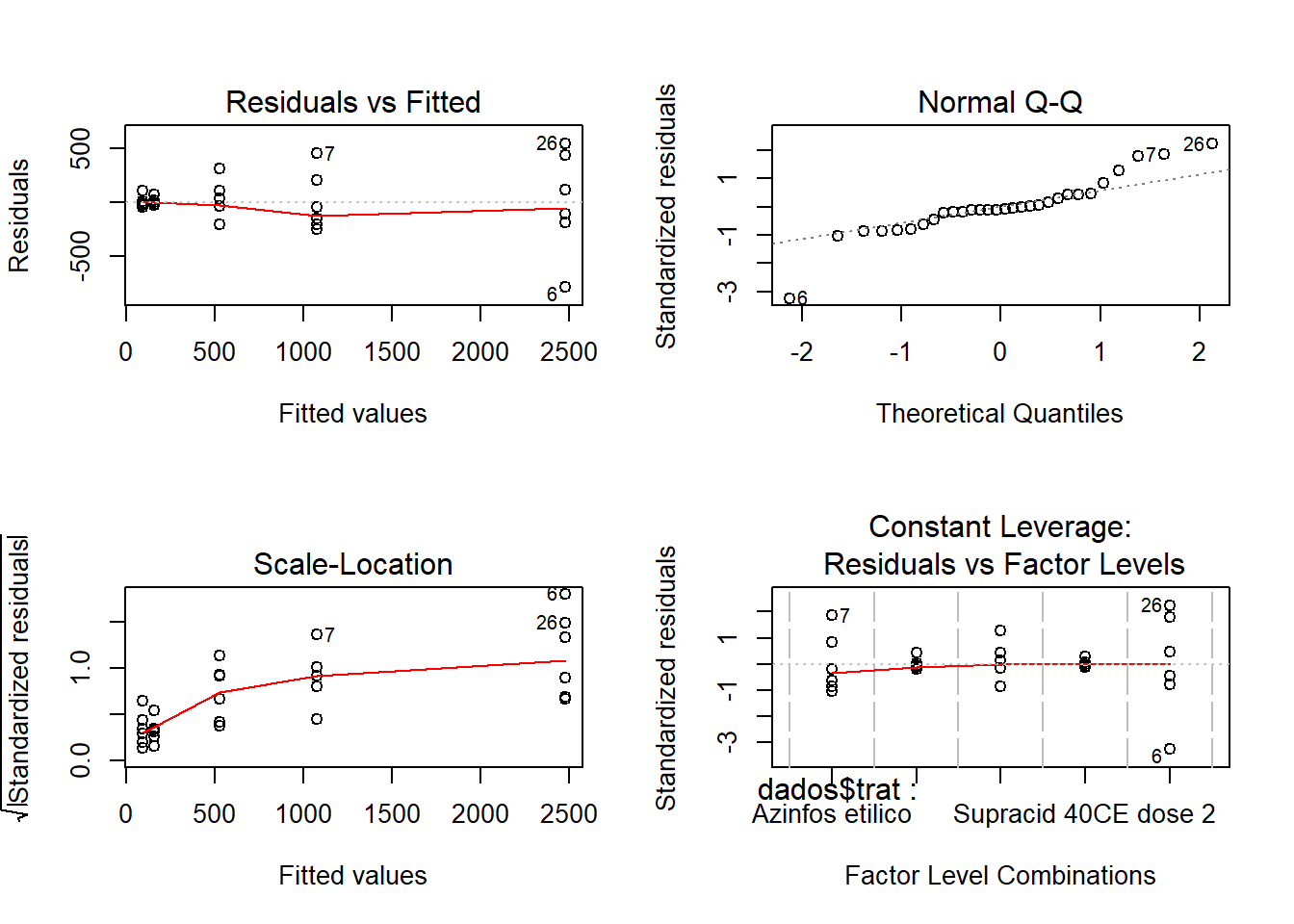
Analisando a figura acima sugere que o principal problema deste conjunto de dados pode ser a heterosdasticidade. A variabilidade dos erros apresentam um forma de cone.

Teste das pressuposições da análise de variância**:

# Teste de Bartllet para homocedasticidade
bartlett.test(m0$res, dados$trat)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  m0$res and dados$trat
## Bartlett's K-squared = 29.586, df = 4, p-value = 5.942e-06

Como observamos uma significância estatística neste resultado, devemos rejeitar a hipótese nula de que as variâncias sejam as mesmas em todos os níveis do fator.

Teste de Shapiro-Wilk para Normalidade:

shapiro.test(m0$res)

## 
##  Shapiro-Wilk normality test
## 
## data:  m0$res
## W = 0.89608, p-value = 0.006742

8.1.3 Transformação de dados

Tranformação de dados é uma das possíveis formas de contornar o problema de dados que não obedecem os pressupostos da análise de variância. Vamos ver como isto poder ser feito com o programa R.

Nos resultados acima vemos que a homogeneidade de variâncias foi rejeitada. Para tentar contornar o problema podemos utilizar catálogos de transformação:

Transformação de raiz quadrada: frequentemente utilizada para dados de contagens, que geralmente seguem a distribuição de Poison, na qual a média é igual a variância. Quando ocorrem zeros ou valores baixos (menores que 10 ou 15), as transformação recomendadas são raiz quadrada + 0,5 ou 1,0.
Transformação angular: recomendável para dados expressos em porcentagens, que geralmente segue distribuição binomial.
Transformação logarítima: utilizada quando é constatada certa proporcionalidade entre as médias e os desvios padrões dos diversos tratamentos:

m1 <- lm (log(dados$pulgoes) ~ dados$trat)

8.1.3.1 Transformação de dados BOX-COX

Para tentar contornar o problema vamos usar a transformação Box-Cox, que consiste em transformar os dados de acordo com uma expressão.

A função boxcox() do pacote MASS calcula a verossimilhança perfilhada do parâmetro. Devemos escolher o valor que maximiza esta função. Nos comandos a seguir começamos carregando o pacote MASS e depois obtemos o gráfico da verossimilhança perfilhada. Como estamos interessados no máximo fazermos um novo gráfico com um zoom na região de interesse:

require(MASS)

## Loading required package: MASS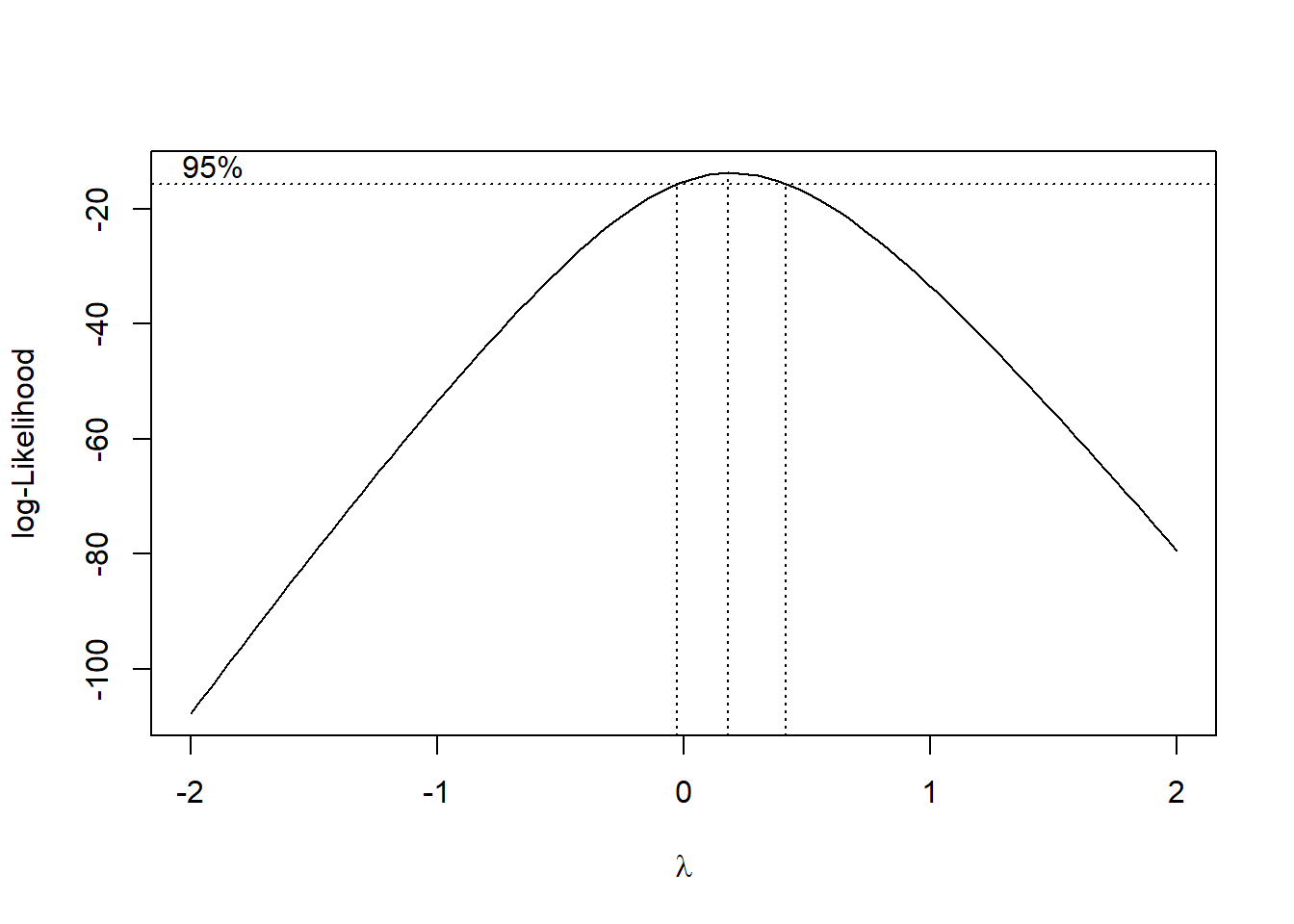

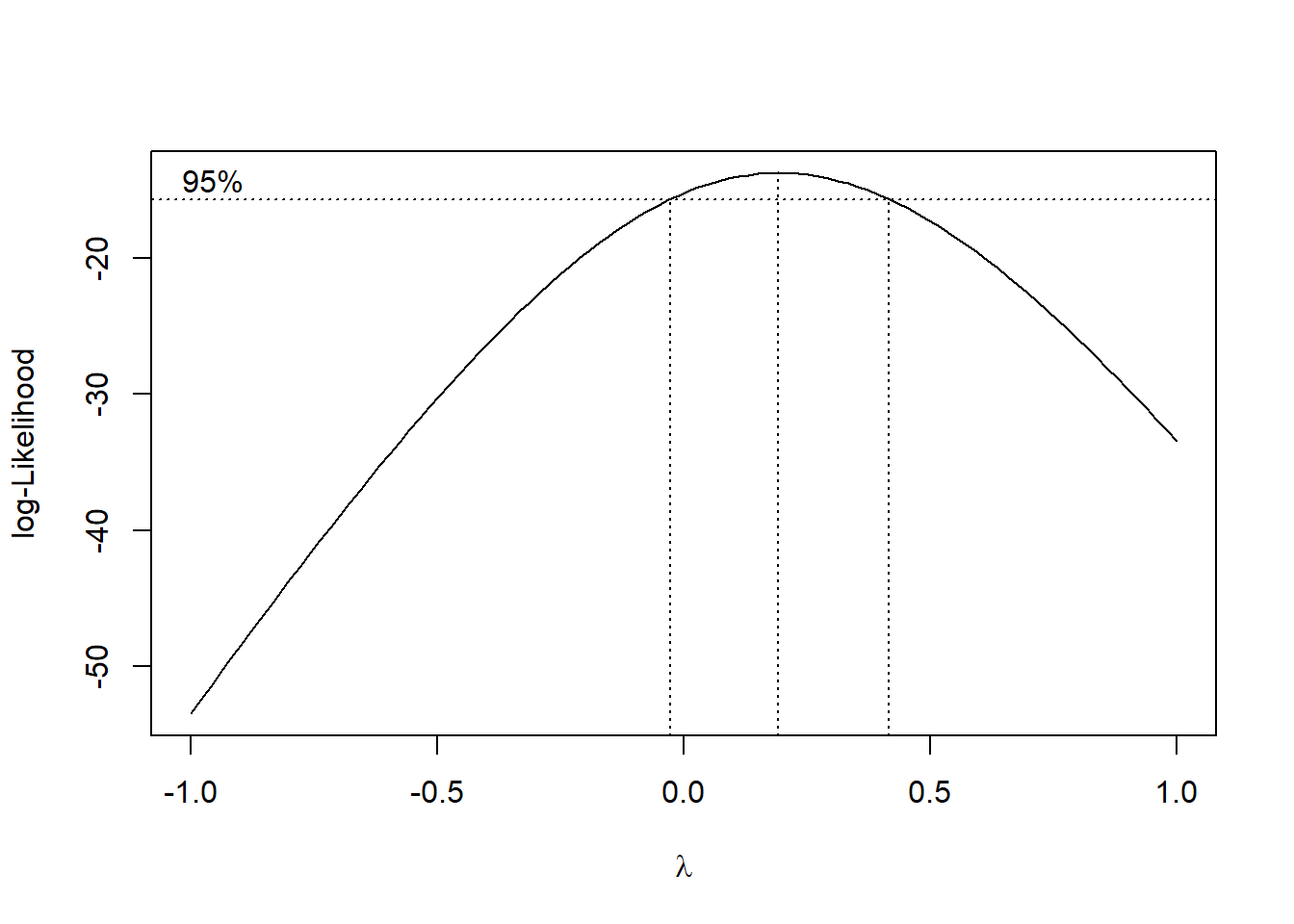
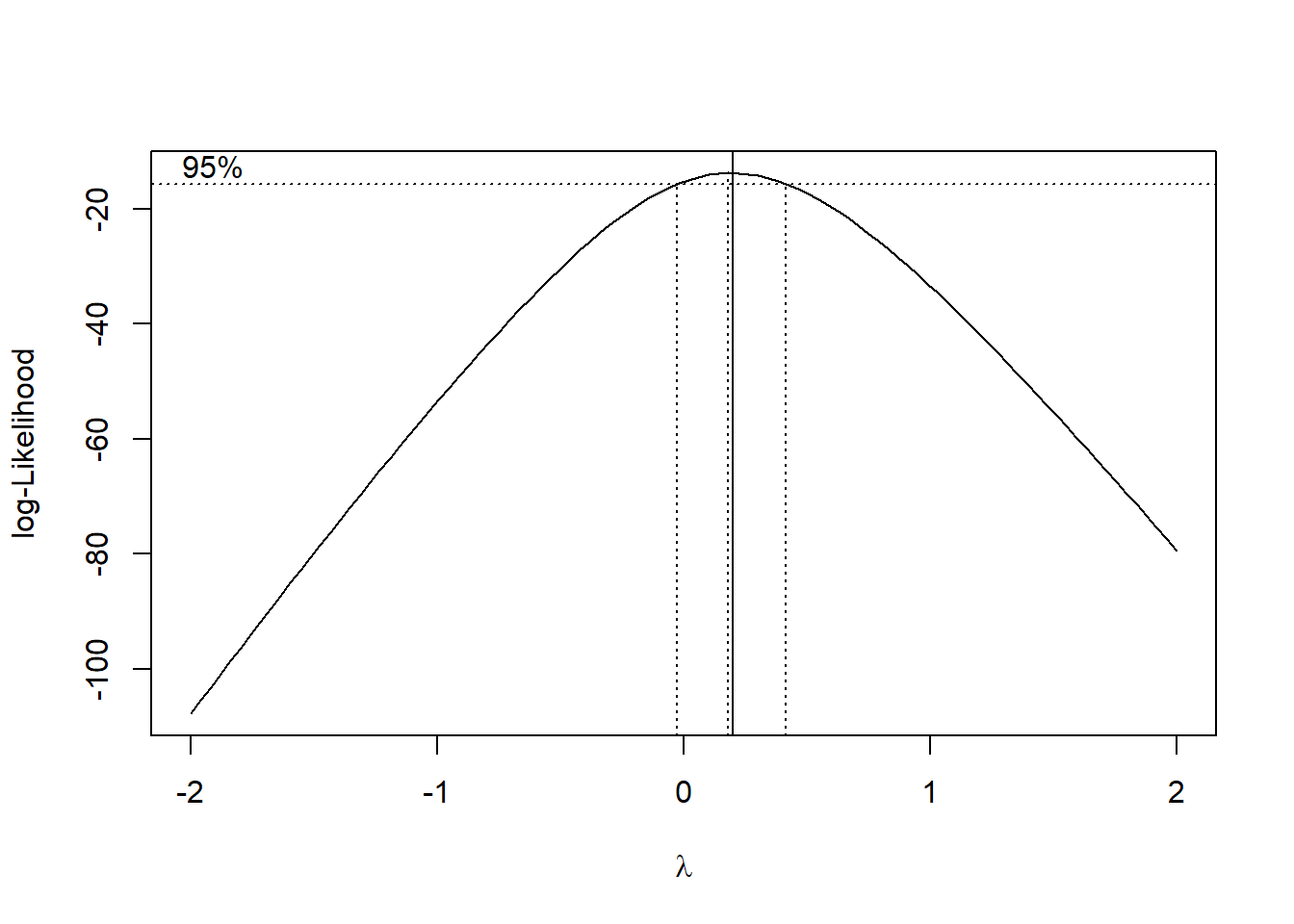
  boxcox(m0)

  #Com zoom
  boxcox(m0, lam = seq(-1, 1, 1/10))

  boxcox(m0)
  abline(v=0.2)
  locator()

8.1.3.2 Análise de variância - Ajuste com a variável transformada.

m1 <- lm (dados$pulgoes^0.2 ~ dados$trat, data = dados)

análise gráfica dos resíduos

par(mfrow = c(2,2))
plot(m1)

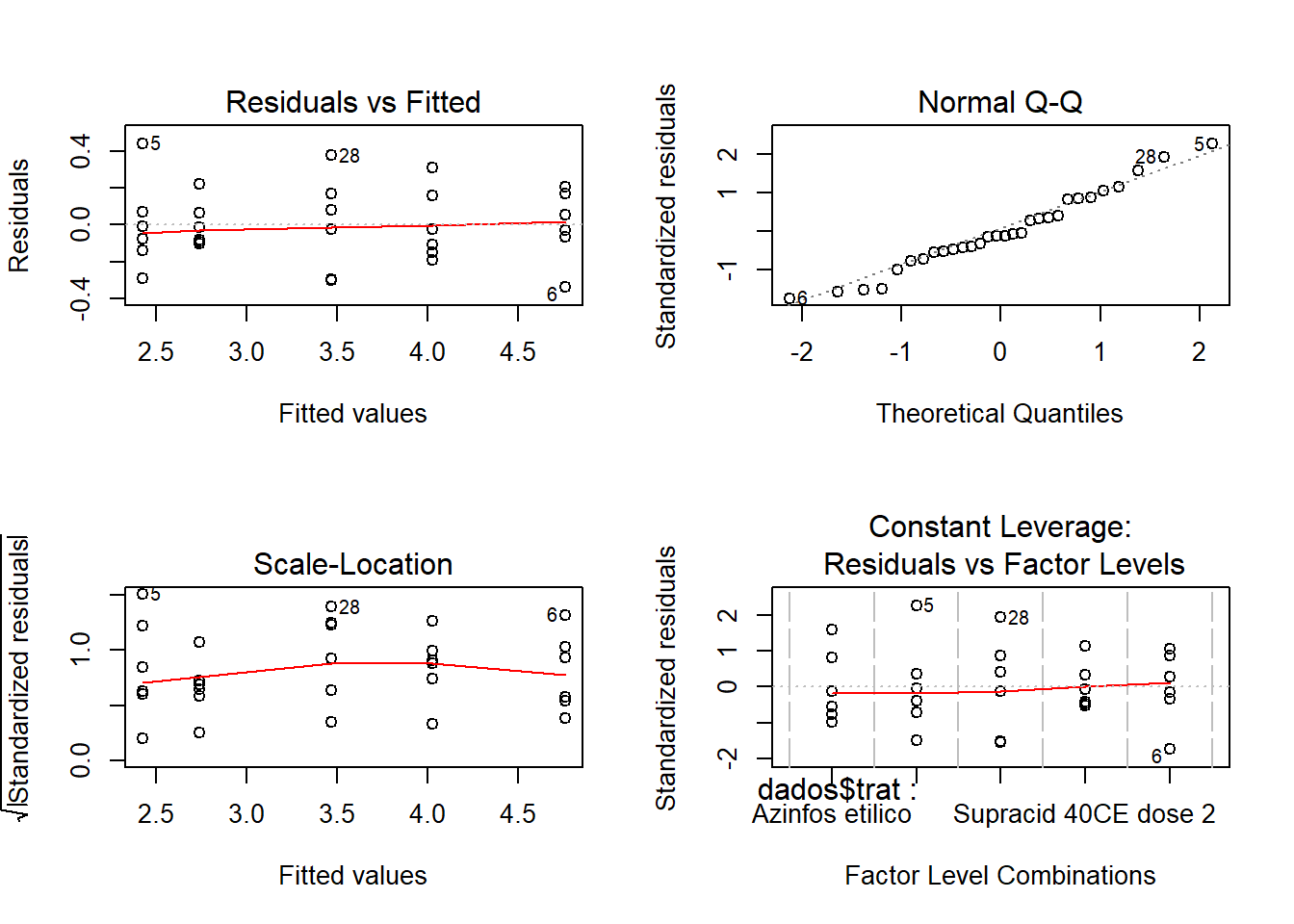
Os pressupostos foram atendindos

Teste de Shapiro-Wilk para Normalidade:

shapiro.test(m1$res)

## 
##  Shapiro-Wilk normality test
## 
## data:  m1$res
## W = 0.97288, p-value = 0.6207

Teste de Bartllet para homocedasticidade:

bartlett.test(m1$res, dados$trat)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  m1$res and dados$trat
## Bartlett's K-squared = 2.7641, df = 4, p-value = 0.598

Resumo do modelo ajustado - Contraste :

summary(m1)

## 
## Call:
## lm(formula = dados$pulgoes^0.2 ~ dados$trat, data = dados)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.33971 -0.10602 -0.02286  0.14069  0.44317 
## 
## Coefficients:
##                                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                     4.02268    0.08709  46.191  < 2e-16 ***
## dados$tratDiazinon 60CE        -1.60093    0.12316 -12.999 1.27e-12 ***
## dados$tratSupracid 40CE dose 1 -0.55418    0.12316  -4.500 0.000136 ***
## dados$tratSupracid 40CE dose 2 -1.28606    0.12316 -10.442 1.33e-10 ***
## dados$tratTestemunha            0.73703    0.12316   5.984 3.00e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2133 on 25 degrees of freedom
## Multiple R-squared:   0.95,  Adjusted R-squared:  0.942 
## F-statistic: 118.8 on 4 and 25 DF,  p-value: 6.978e-16

Resumo do modelo ajustado - Contraste em relação a testemunha:

dados$trat <- relevel(dados$trat, "Testemunha")

m1 <- lm (dados$pulgoes^0.2 ~ dados$trat, data = dados)

summary(m1)

## 
## Call:
## lm(formula = dados$pulgoes^0.2 ~ dados$trat, data = dados)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.33971 -0.10602 -0.02286  0.14069  0.44317 
## 
## Coefficients:
##                                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                     4.75972    0.08709  54.654  < 2e-16 ***
## dados$tratAzinfos etilico      -0.73703    0.12316  -5.984 3.00e-06 ***
## dados$tratDiazinon 60CE        -2.33797    0.12316 -18.983 2.31e-16 ***
## dados$tratSupracid 40CE dose 1 -1.29122    0.12316 -10.484 1.23e-10 ***
## dados$tratSupracid 40CE dose 2 -2.02310    0.12316 -16.426 6.62e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2133 on 25 degrees of freedom
## Multiple R-squared:   0.95,  Adjusted R-squared:  0.942 
## F-statistic: 118.8 on 4 and 25 DF,  p-value: 6.978e-16

8.1.4 Aplicando teste de Tukey para comparar médias

No R, o teste de Tukey é apresentado através de intervalos de confiança. A interpretação é: se o intervalo de confiança para a diferença entre duas médias não incluir o valor zero, significa que se rejeita a hipótese nula, caso contrário, não se rejeita. O resultado pode ser visto através de uma tabela e/ou graficamente:

m1 <- aov (dados$pulgoes^0.2 ~ dados$trat, data = dados)

dados.tu <- TukeyHSD (m1)

print(dados.tu)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = dados$pulgoes^0.2 ~ dados$trat, data = dados)
## 
## $`dados$trat`
##                                                 diff         lwr        upr
## Azinfos etilico-Testemunha                -0.7370340 -1.09874544 -0.3753225
## Diazinon 60CE-Testemunha                  -2.3379681 -2.69967961 -1.9762567
## Supracid 40CE dose 1-Testemunha           -1.2912155 -1.65292701 -0.9295041
## Supracid 40CE dose 2-Testemunha           -2.0230984 -2.38480982 -1.6613869
## Diazinon 60CE-Azinfos etilico             -1.6009342 -1.96264562 -1.2392227
## Supracid 40CE dose 1-Azinfos etilico      -0.5541816 -0.91589302 -0.1924701
## Supracid 40CE dose 2-Azinfos etilico      -1.2860644 -1.64777584 -0.9243529
## Supracid 40CE dose 1-Diazinon 60CE         1.0467526  0.68504114  1.4084641
## Supracid 40CE dose 2-Diazinon 60CE         0.3148698 -0.04684168  0.6765812
## Supracid 40CE dose 2-Supracid 40CE dose 1 -0.7318828 -1.09359428 -0.3701714
##                                               p adj
## Azinfos etilico-Testemunha                0.0000277
## Diazinon 60CE-Testemunha                  0.0000000
## Supracid 40CE dose 1-Testemunha           0.0000000
## Supracid 40CE dose 2-Testemunha           0.0000000
## Diazinon 60CE-Azinfos etilico             0.0000000
## Supracid 40CE dose 1-Azinfos etilico      0.0011809
## Supracid 40CE dose 2-Azinfos etilico      0.0000000
## Supracid 40CE dose 1-Diazinon 60CE        0.0000001
## Supracid 40CE dose 2-Diazinon 60CE        0.1099096
## Supracid 40CE dose 2-Supracid 40CE dose 1 0.0000307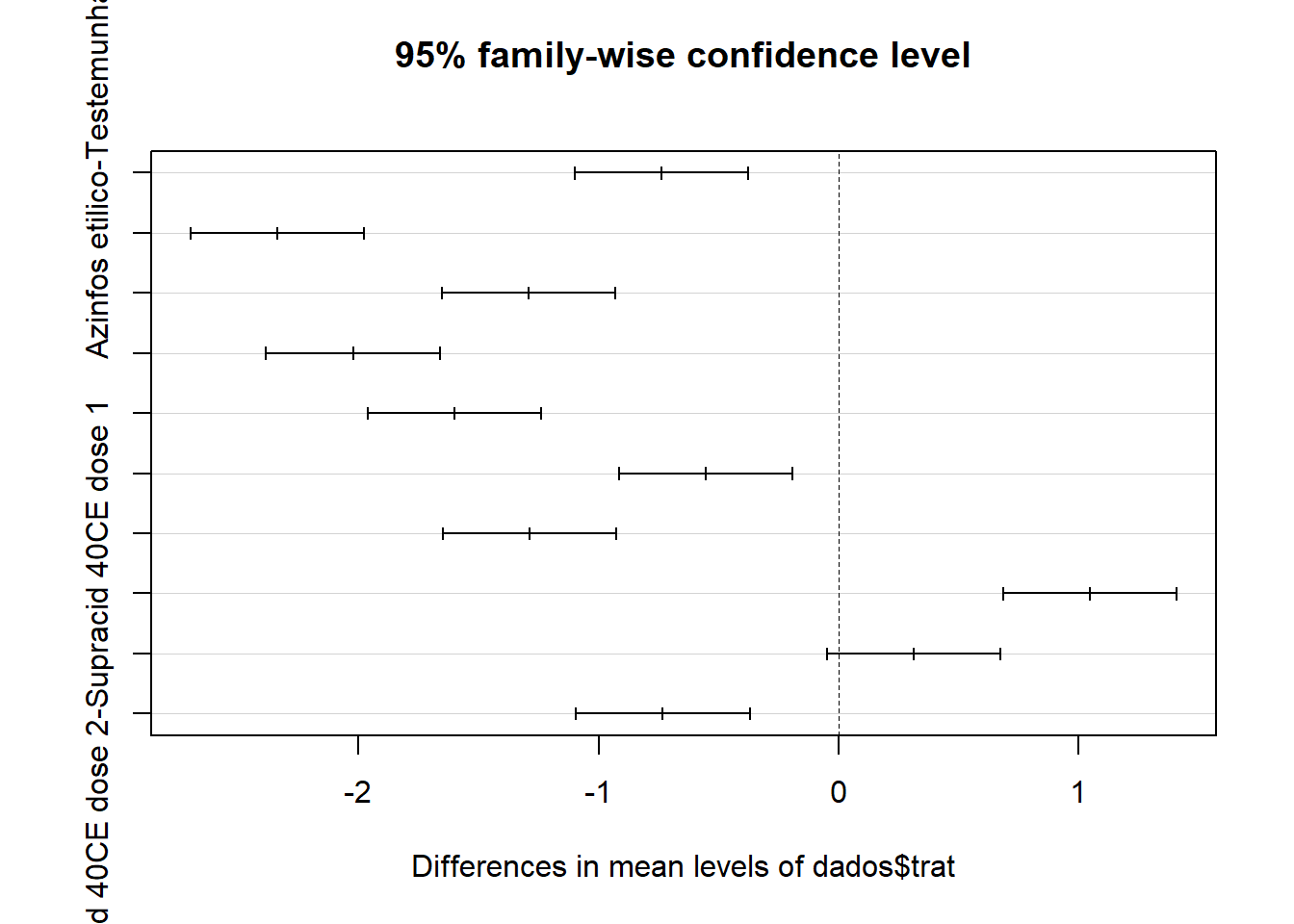

plot(dados.tu)

Teste Tukey com pacote Agricolae

library(agricolae)

summary(m1)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## dados$trat   4 21.629   5.407   118.8 6.98e-16 ***
## Residuals   25  1.138   0.046                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

tu <- HSD.test(y = dados$pulgoes^0.2,
         trt = dados$trat,
         MSerror = deviance(m1)/df.residual(m1), #quadrado médio do residuo
         DFerror = df.residual(m1),
         console = T)

## 
## Study: dados$pulgoes^0.2 ~ dados$trat
## 
## HSD Test for dados$pulgoes^0.2 
## 
## Mean Square Error:  0.04550677 
## 
## dados$trat,  means
## 
##                      dados.pulgoes.0.2       std r      Min      Max
## Azinfos etilico               4.022682 0.1967278 6 3.830812 4.332792
## Diazinon 60CE                 2.421748 0.2492525 6 2.131526 2.864913
## Supracid 40CE dose 1          3.468500 0.2678917 6 3.163821 3.846471
## Supracid 40CE dose 2          2.736617 0.1264052 6 2.634879 2.959410
## Testemunha                    4.759716 0.1973855 6 4.420008 4.965939
## 
## Alpha: 0.05 ; DF Error: 25 
## Critical Value of Studentized Range: 4.153363 
## 
## Minimun Significant Difference: 0.3617115 
## 
## Treatments with the same letter are not significantly different.
## 
##                      dados$pulgoes^0.2 groups
## Testemunha                    4.759716      a
## Azinfos etilico               4.022682      b
## Supracid 40CE dose 1          3.468500      c
## Supracid 40CE dose 2          2.736617      d
## Diazinon 60CE                 2.421748      d

str(tu)

## List of 5
##  $ statistics:'data.frame':  1 obs. of  5 variables:
##   ..$ MSerror: num 0.0455
##   ..$ Df     : int 25
##   ..$ Mean   : num 3.48
##   ..$ CV     : num 6.13
##   ..$ MSD    : num 0.362
##  $ parameters:'data.frame':  1 obs. of  5 variables:
##   ..$ test            : Factor w/ 1 level "Tukey": 1
##   ..$ name.t          : Factor w/ 1 level "dados$trat": 1
##   ..$ ntr             : int 5
##   ..$ StudentizedRange: num 4.15
##   ..$ alpha           : num 0.05
##  $ means     :'data.frame':  5 obs. of  8 variables:
##   ..$ dados$pulgoes^0.2: num [1:5] 4.02 2.42 3.47 2.74 4.76
##   ..$ std              : num [1:5] 0.197 0.249 0.268 0.126 0.197
##   ..$ r                : int [1:5] 6 6 6 6 6
##   ..$ Min              : num [1:5] 3.83 2.13 3.16 2.63 4.42
##   ..$ Max              : num [1:5] 4.33 2.86 3.85 2.96 4.97
##   ..$ Q25              : num [1:5] 3.88 2.3 3.24 2.65 4.7
##   ..$ Q50              : num [1:5] 3.96 2.38 3.5 2.69 4.77
##   ..$ Q75              : num [1:5] 4.14 2.47 3.61 2.78 4.9
##  $ comparison: NULL
##  $ groups    :'data.frame':  5 obs. of  2 variables:
##   ..$ dados$pulgoes^0.2: num [1:5] 4.76 4.02 3.47 2.74 2.42
##   ..$ groups           : Factor w/ 4 levels "a","b","c","d": 1 2 3 4 4
##  - attr(*, "class")= chr "group"

tu$groups

##                      dados$pulgoes^0.2 groups
## Testemunha                    4.759716      a
## Azinfos etilico               4.022682      b
## Supracid 40CE dose 1          3.468500      c
## Supracid 40CE dose 2          2.736617      d
## Diazinon 60CE                 2.421748      d

write.table(tu$groups,
            "tab.xls",
            sep = "\t",
            quote = F,
            row.names = F)

8.1.5 Aplicando teste para agrupar médias

carregando a biblioteca necessária

#install.packages("laercio")
require(laercio)

## Loading required package: laercio

Teste de Duncan:

LDuncan (m1, "dados$trat")

## 
##  DUNCAN TEST TO COMPARE MEANS 
##  
##  Confidence Level:  0.95 
##  Dependent Variable:  dados$pulgoes^0.2
##  Variation Coefficient:  6.126714 % 
##  
## 
##  Independent Variable:  dados$trat 
##   Factors              Means                 
##   Testemunha           4.75971565312899 a    
##   Azinfos etilico      4.02268167030532  b   
##   Supracid 40CE dose 1 3.46850010815533   c  
##   Supracid 40CE dose 2 2.73661729164913    d 
##   Diazinon 60CE        2.42174750727391     e

LTukey (m1, "dados$trat")

## 
##  TUKEY TEST TO COMPARE MEANS 
##  
##  Confidence level:  0.95 
##  Dependent variable:  dados$pulgoes^0.2
##  Variation Coefficient:  6.126714 % 
##  
## Independent variable:  dados$trat 
##   Factors              Means                
##   Testemunha           4.75971565312899 a   
##   Azinfos etilico      4.02268167030532  b  
##   Supracid 40CE dose 1 3.46850010815533   c 
##   Supracid 40CE dose 2 2.73661729164913    d
##   Diazinon 60CE        2.42174750727391    d
## 
##

Pacote para análise de experimentos:

library(ExpDes.pt)

## 
## Attaching package: 'ExpDes.pt'

## The following object is masked from 'package:MASS':
## 
##     ginv

## The following objects are masked from 'package:agricolae':
## 
##     lastC, order.group, tapply.stat

## The following object is masked from 'package:stats':
## 
##     ccf

Recursos adicionais para comparações múltiplas

Outros procedimentos serão implementados em pacotes contribuídos do R. Entre estes encontra-se os pacotes multcomp e multcompView que implementam diversos outros procedimentos e gráficos para visualizações dos resultados. Vale notar que estes pacotes devem ser instalados com a opção dependencies=TRUE para garantir plena funcionalidade pois suas funções dependem de diversos outros pacotes:

#install.packages("multcompView", dep = TRUE) 
require(multcomp)

## Loading required package: multcomp

## Loading required package: mvtnorm

## Loading required package: survival

## Loading required package: TH.data

## 
## Attaching package: 'TH.data'

## The following object is masked from 'package:MASS':
## 
##     geyser

require(multcompView)

## Loading required package: multcompView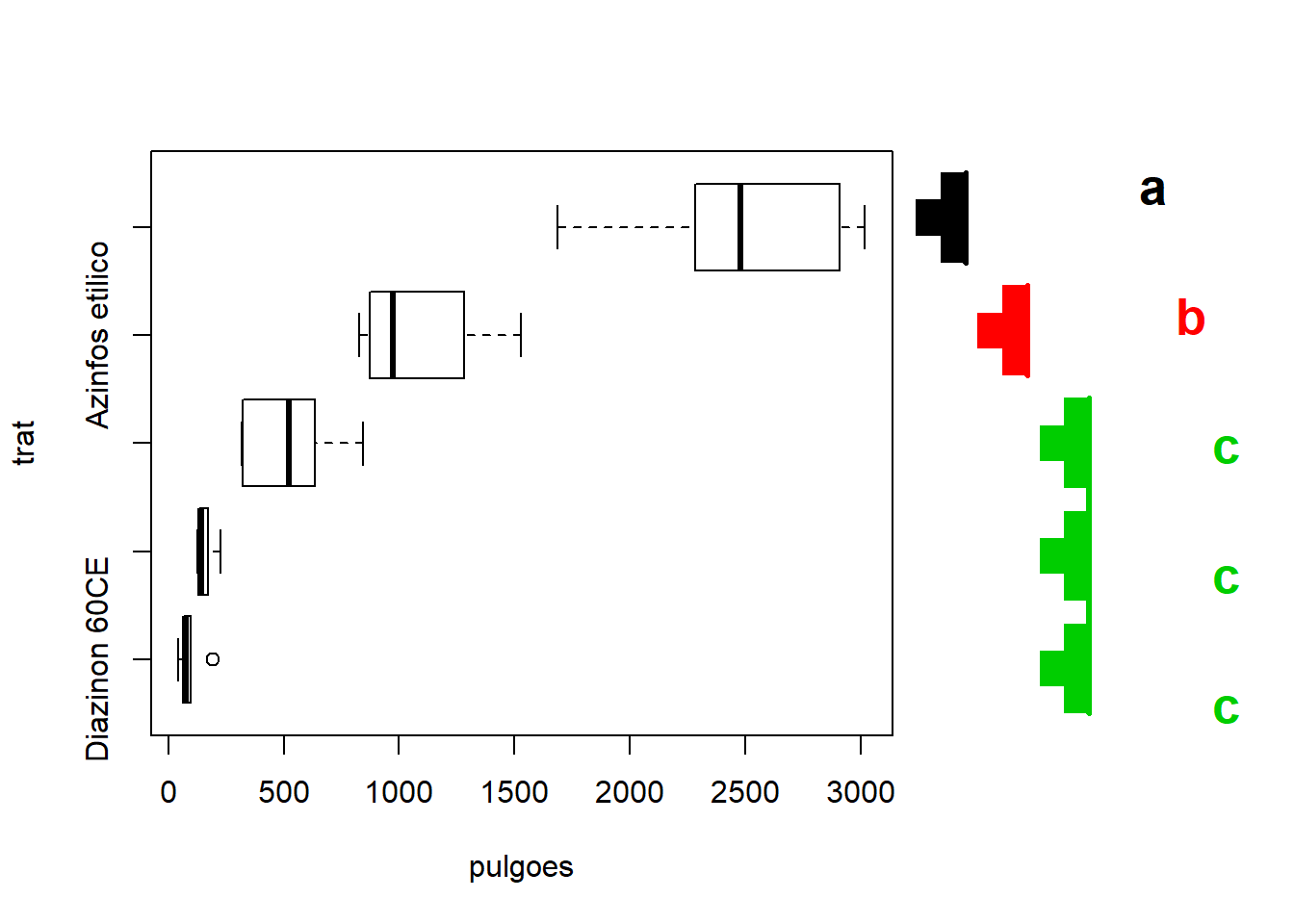

multcompBoxplot(pulgoes ~ trat, data = dados, compFn = "TukeyHSD", decreasing = FALSE)

8.1.6 Referência

MELO, M. P.; PETERNELI, L. A. Conhecendo o R: Um visão mais que estatística. Viçosa, MG: UFV, 2013. 222p. Cap. 1.

BANZATTO, D. A; KRONKA, S. N. Experimentação agrícola. Jaboticabal, SP: FUNEP, 2006, 237p.

ZEVIANI, W. M. estatística Básica e Experimentação no R. 45p.

http://www.leg.ufpr.br/~paulojus/

8.2 Delineamento em bloco casualizado

O delineamento em blocos casualizados (DBC) tem três princípios basicos de experimentação:

repetição
casualização
controle local

É o deliamento mais utilizado de todos os delineamentos. Ele é utilizado quando há heterogeneidade nas condições experimentais. Nesse caso divide-se o material experimental, ou amostra, em bloco homogêneos de forma a contemplar as diferenças entre grupos. A ANOVA associada a este modelo de experimento é também conhecida como Two Way ANOVA.

8.2.1 Análise de experimento DBC

Resultados de um experimento instalado na Fazenda Chapadão, no município de Angatuba - SP. O delineamento experimental foi o de blocos casualizados, sendo as parcelas constituídas de 4 plantas espaçadas de 6 x 7 metros, com 12 anos de idade na época da instalação do experimento.

Importando dados:

dados <- read.table("https://www.dropbox.com/s/9woiye3ce9twp78/BanzattoQd4.5.2.txt?dl=1")

conferir se temos fatores para fazer a análise de variância:

str(dados)

## 'data.frame':    20 obs. of  3 variables:
##  $ promalin: Factor w/ 5 levels "12.5","12.5+12.5",..: 1 3 4 2 5 1 3 4 2 5 ...
##  $ bloco   : Factor w/ 4 levels "I","II","III",..: 1 1 1 1 1 2 2 2 2 2 ...
##  $ peso    : num  142 140 141 151 154 ...

Lembramos que o peso deve ter conteúdo numérico e o promalin e bloco deve ser fator:

dados$promalin<-as.factor(dados$promalin)
dados$bloco<-as.numeric(dados$bloco)

Verificação gráfica**:

require(lattice)

## Loading required package: lattice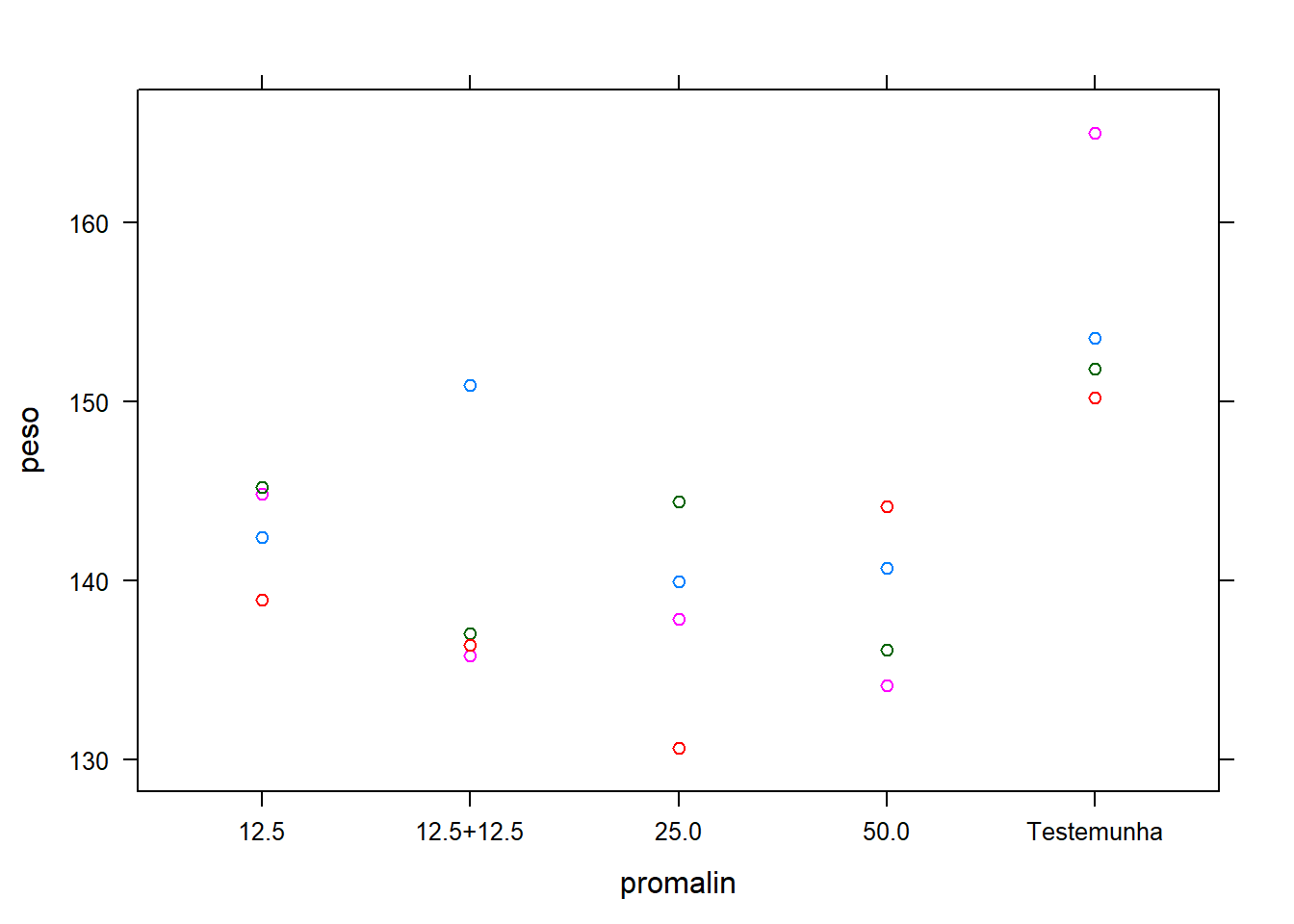

xyplot(peso ~ promalin, 
        groups = bloco, 
        data= dados)

O efeito do bloco é aditivo?

Ligar as observações com o mesmo bloco com a função type ="o":

xyplot(peso ~ reorder(promalin, peso), 
        groups = bloco, 
        data= dados,
        type = "o")

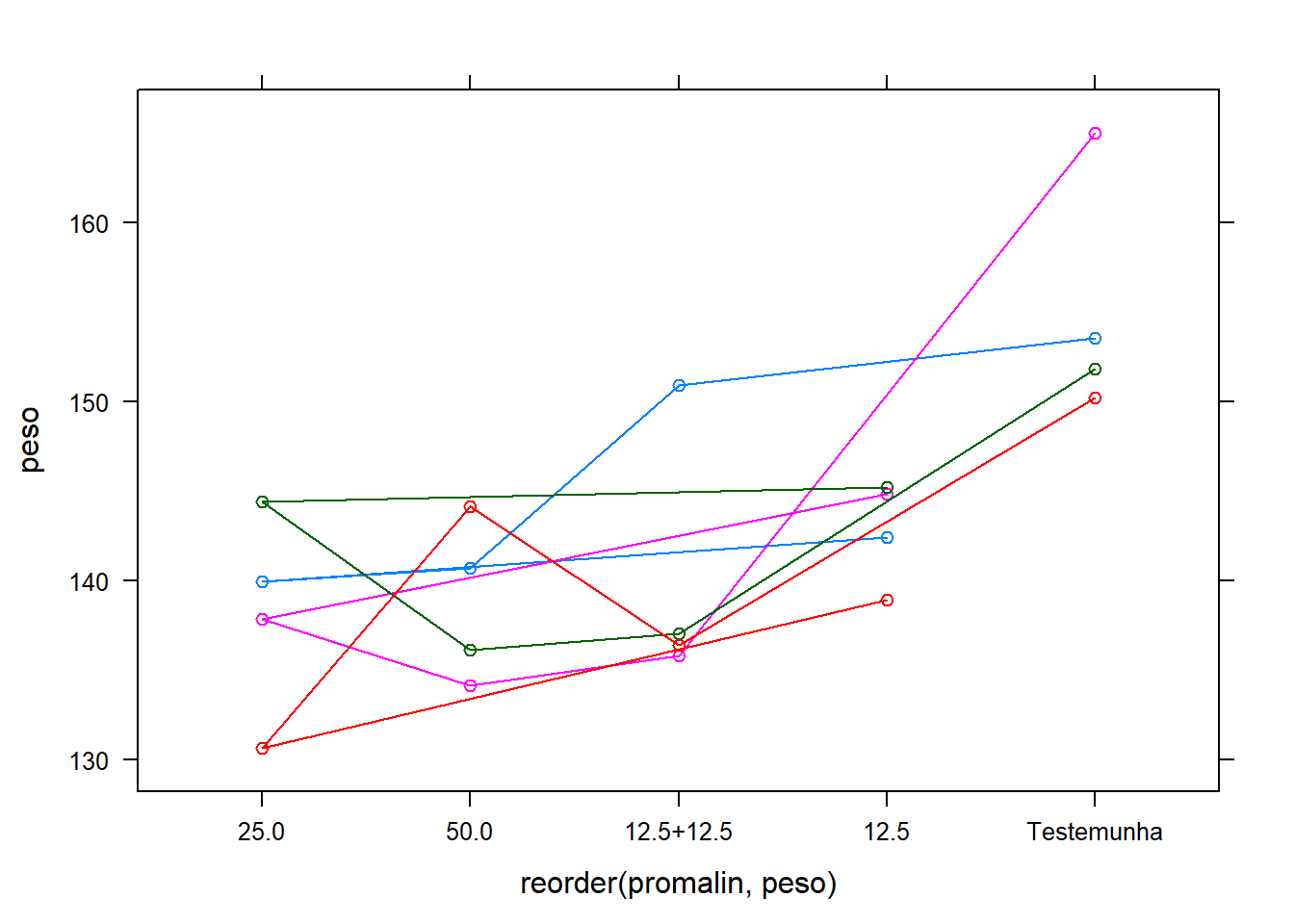
Reordenar os tratamentos:

require(plyr)

## Loading required package: plyr

dados$promalin <- with(dados, reorder(promalin, peso))
dados <- arrange(dados, promalin, bloco)

Gráficos reordenados de menor média a maior média por tratamento:

xyplot(peso ~ reorder(promalin, peso), 
        groups = bloco, 
        data= dados,
        type = "o")

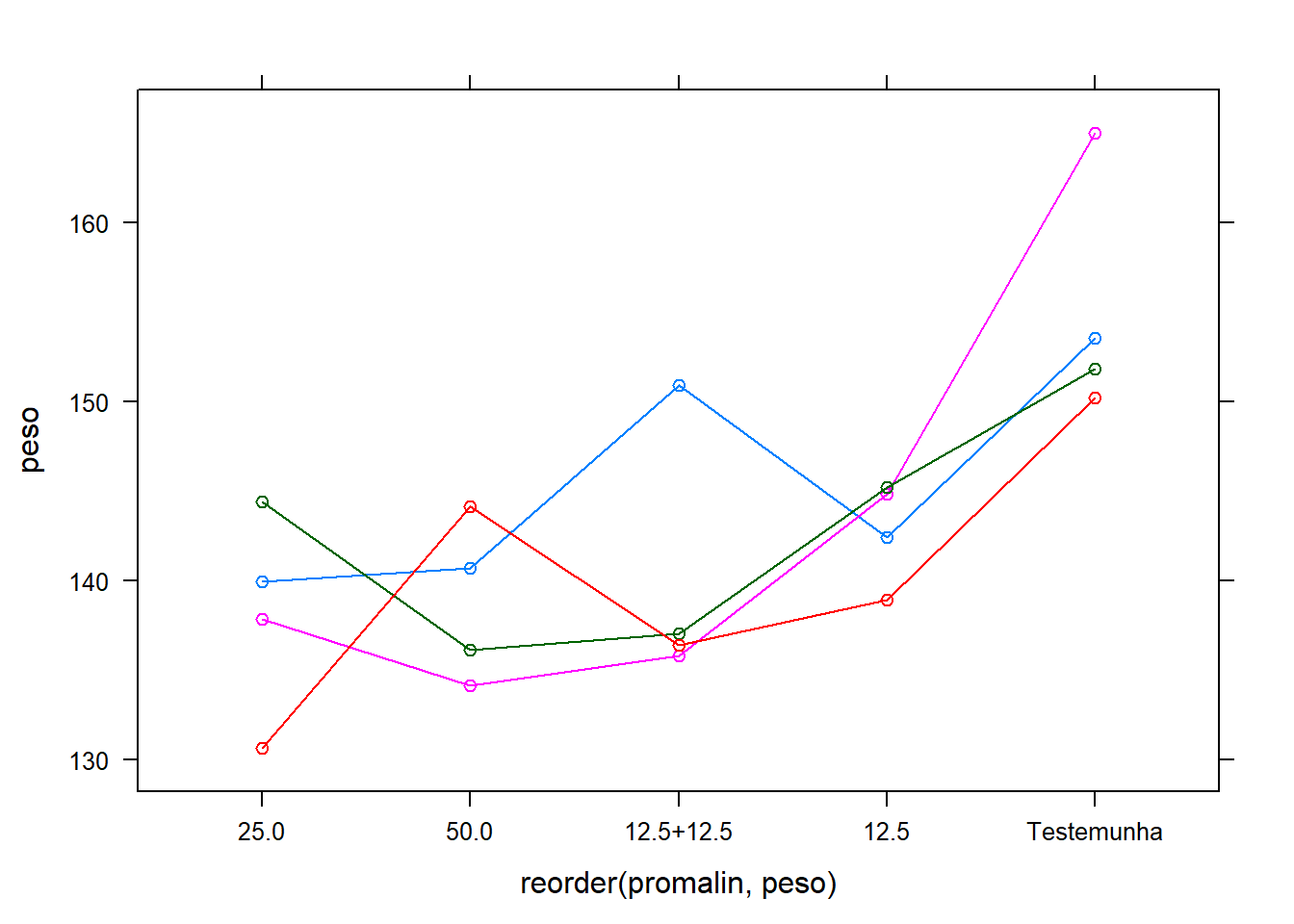
8.2.1.1 Análise de variância

Fazendo a análise de variância:

m0 <- lm (dados$peso ~ dados$bloco + dados$promalin, data = dados)

anova(m0)

## Analysis of Variance Table
## 
## Response: dados$peso
##                Df Sum Sq Mean Sq F value   Pr(>F)   
## dados$bloco     1  71.57  71.572  2.4574 0.139291   
## dados$promalin  4 788.95 197.238  6.7721 0.002994 **
## Residuals      14 407.75  29.125                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Extraíndo o coeficiente de variação:

require(agricolae)
cv.model(m0)

## [1] 3.774477

Análise gráfica dos resíduos:

par(mfrow= c(2,2))
plot(m0)

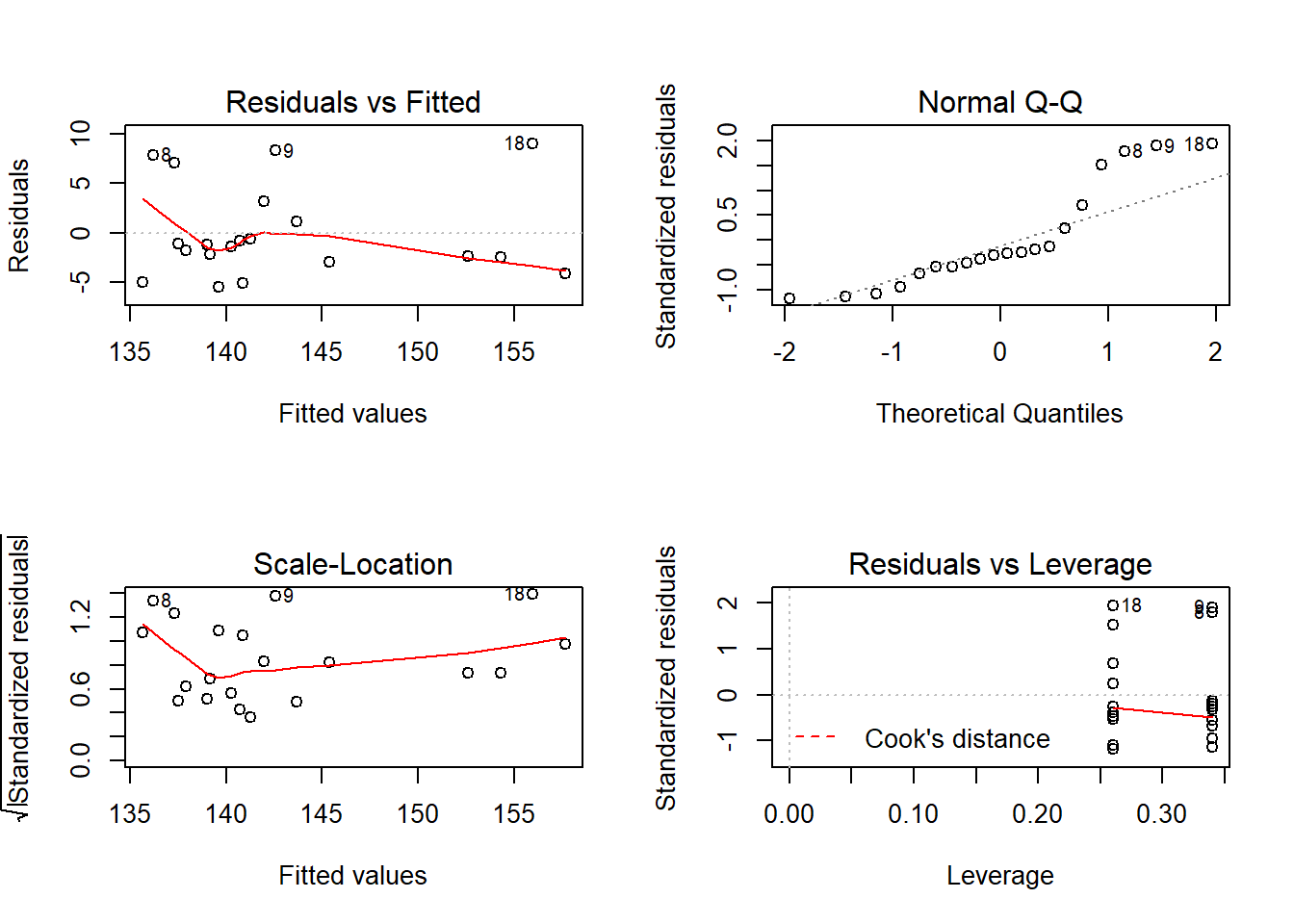
Analisando a figura acima sugere que o principal problema deste conjunto de dados pode ser a não normalidade.

8.2.1.1.1 Teste das pressuposições da análise de variância

8.2.1.1.1.0.1 Teste de Bartllet para homocedasticidade:

bartlett.test(m0$res, dados$promalin)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  m0$res and dados$promalin
## Bartlett's K-squared = 1.7485, df = 4, p-value = 0.7819

Como observamos uma não significância estatística neste resultado (p-value = 0.7819), devemos aceitar a hipótese nula de que as variâncias sejam as mesma em todos os níveis do fator.

8.2.1.1.1.0.2 Teste de Shapiro-Wilk para Normalidade:

shapiro.test(m0$res)

## 
##  Shapiro-Wilk normality test
## 
## data:  m0$res
## W = 0.855, p-value = 0.006472

Como observamos uma significância estatística neste resultado (p-value = 0.006472), devemos rejeitar a hipótese nula de que os resíduos tedem a distruibuição normal.

8.2.1.2 Transformação de dados

8.2.1.2.1 Transformação de dados com o BOX-COX

Para tentar contornar o problema vamos usar a transformação Box-Cox, que consiste em transformar os dados de acordo com uma expressão.

A função boxcox() do pacote MASS calcula a verossimilhança perfilhada do parâmetro lambda. Devemos escolher o valor que maximiza esta função. Nos comandos a seguir começamos carregando o pacote MASS e depois obtemos o gráfico da verossimilhança perfilhada. Como estamos interessados no máximo, vamos fazer um novo gráfico com um zoom na região de interesse:

require(MASS) 
  boxcox(m0)

  boxcox(m0, lam = seq(-8, 8, 1/10))

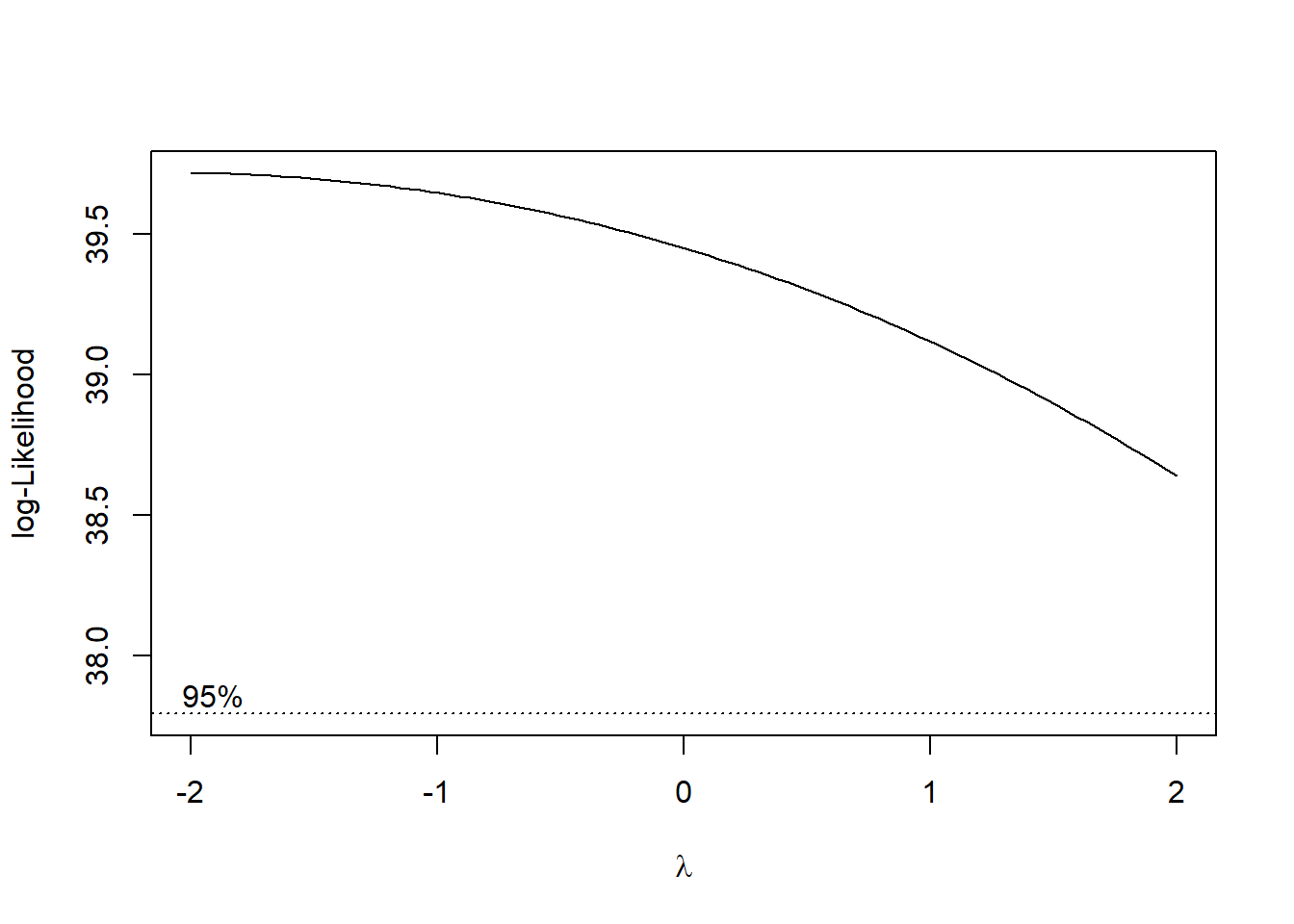
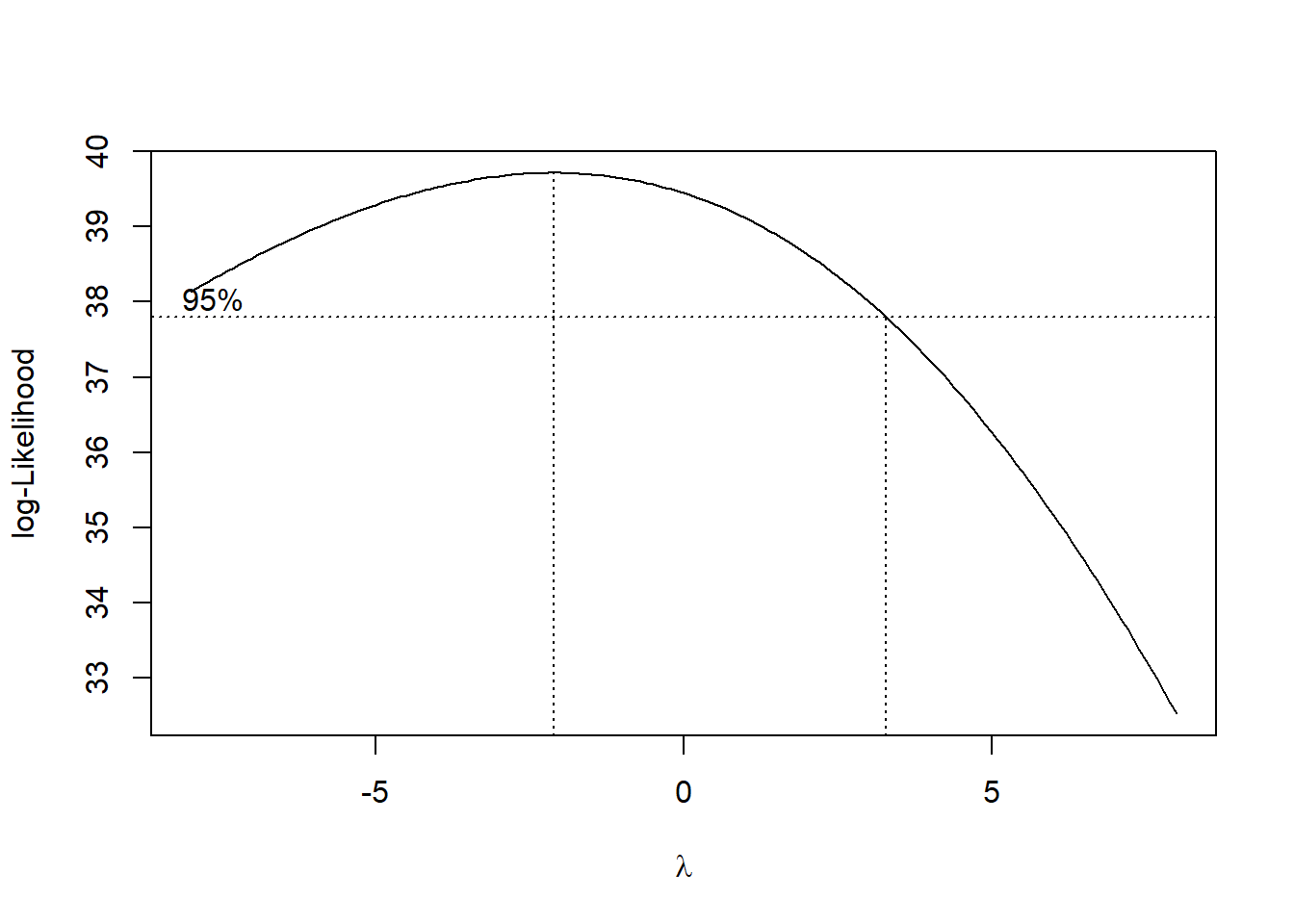
Localizando o ponto máximo:

8.2.1.2.2 Análise de variância - Ajuste com a variável transformada.

m1 <- aov (log(dados$peso) ~ dados$promalin, data = dados)

Anáise gráfica dos resíduos:

par(mfrow = c(2,2))
plot(m1)

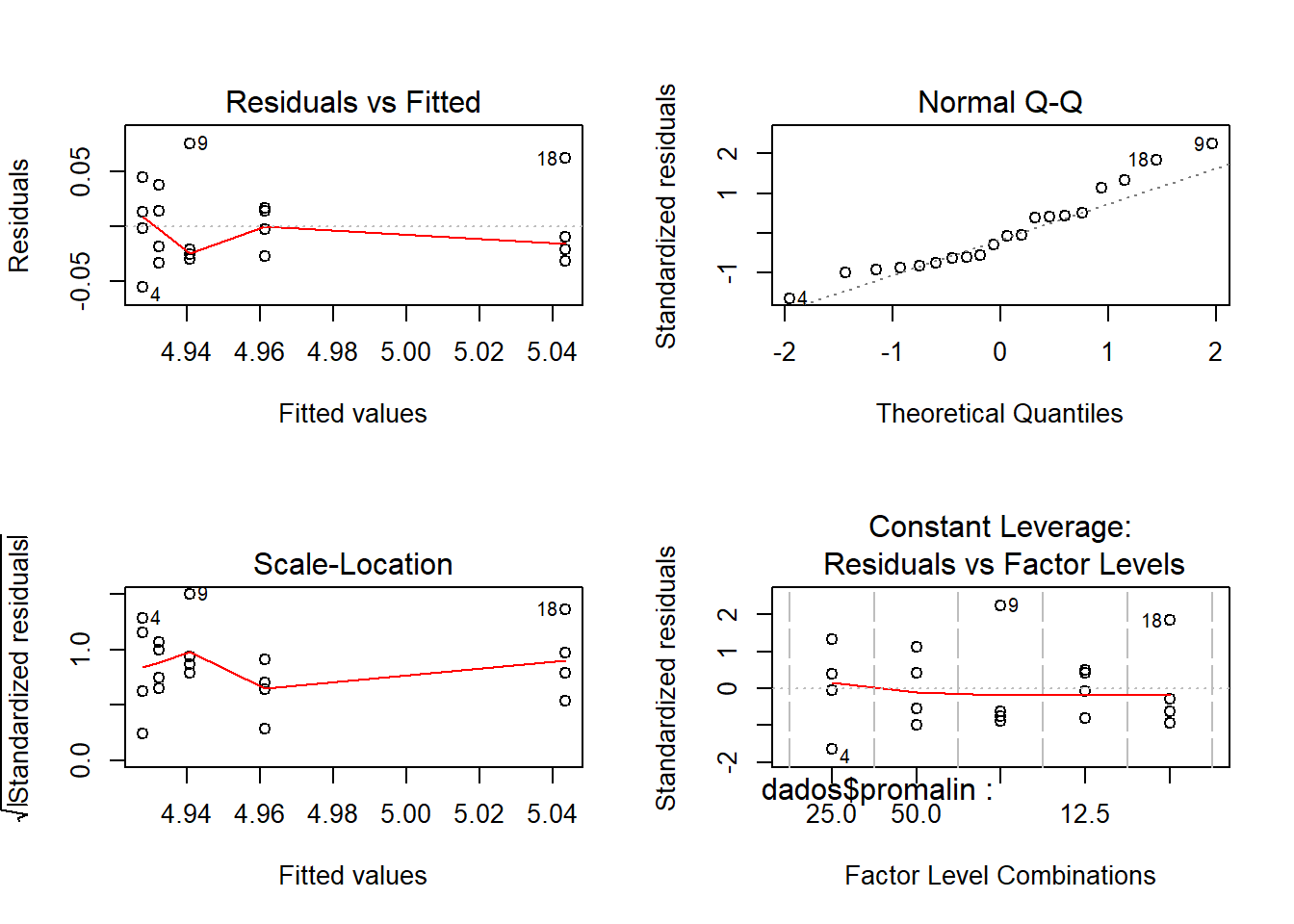
Os pressupostos foram atendindos?

Teste de Shapiro-Wilk para Normalidade:

shapiro.test(m1$res)

## 
##  Shapiro-Wilk normality test
## 
## data:  m1$res
## W = 0.93909, p-value = 0.2305

Teste de Bartllet para homocedasticidade:

bartlett.test(m1$res, dados$promalin)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  m1$res and dados$promalin
## Bartlett's K-squared = 2.1761, df = 4, p-value = 0.7034

anova(m1)

## Analysis of Variance Table
## 
## Response: log(dados$peso)
##                Df   Sum Sq   Mean Sq F value   Pr(>F)   
## dados$promalin  4 0.036571 0.0091428  6.0129 0.004296 **
## Residuals      15 0.022808 0.0015205                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

8.2.2 Pacote para analise de experimentos

library(ExpDes.pt)

Conhecer o pacote ExpDes.pt:

ls("package:ExpDes.pt")

##  [1] "anscombetukey"  "bartlett"       "ccboot"         "ccf"           
##  [5] "dbc"            "dic"            "dql"            "duncan"        
##  [9] "faixas"         "fat2.ad.dbc"    "fat2.ad.dic"    "fat2.dbc"      
## [13] "fat2.dic"       "fat3.ad.dbc"    "fat3.ad.dic"    "fat3.dbc"      
## [17] "fat3.dic"       "ginv"           "graficos"       "han"           
## [21] "lastC"          "layard"         "levene"         "lsd"           
## [25] "lsdb"           "oneilldbc"      "oneillmathews"  "order.group"   
## [29] "order.stat.SNK" "plotres"        "psub2.dbc"      "psub2.dic"     
## [33] "reg.nl"         "reg.poly"       "samiuddin"      "scottknott"    
## [37] "snk"            "tapply.stat"    "tukey"

Utilizando o exemplo anterior:

x <- dbc(trat = dados$promalin,
          bloco = dados$bloco,
          resp = log(dados$peso),
          quali = T,
          mcomp = "tukey")

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL       SQ        QM     Fc   Pr>Fc
## Tratamento  4 0.036571 0.0091428 5.7552 0.00800
## Bloco       3 0.003745 0.0012483 0.7858 0.52459
## Residuo    12 0.019063 0.0015886               
## Total      19 0.059379                         
## ------------------------------------------------------------------------
## CV = 0.8 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos 
## valor-p:  0.005994506 
## ATENCAO: a 5% de significancia, os residuos nao podem ser considerados normais!
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia 
## valor-p:  0.8927087 
## De acordo com o teste de oneillmathews a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
## 
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a     Testemunha      5.043544 
## ab    12.5    4.961465 
##  b    12.5+12.5   4.940843 
##  b    50.0    4.932278 
##  b    25.0    4.927864 
## ------------------------------------------------------------------------

Carregar pacotes:

library(ggplot2)
library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:plyr':
## 
##     arrange, count, desc, failwith, id, mutate, rename, summarise,
##     summarize

## The following object is masked from 'package:MASS':
## 
##     select

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

Cálculo do erro:

erro = summarise(group_by(dados, promalin), 
       avg = mean(peso), sd = sd(peso))

Gerando o gráfico:

ggplot(erro, aes(promalin, avg, fill=promalin))+
  geom_bar(stat="identity")+
  geom_errorbar(aes(ymin=avg-sd, ymax =avg+sd), with=0.1, col="black") +
    xlab("Tratamentos") + 
    ylab("Peso médio dos frutos (g)") + 
  theme_bw() + 
  theme(legend.position="top") +
      annotate("text", label="ab", x=1, y=100, size = 5)  +
      annotate("text", label="b", x=2, y=100, size = 5) +
      annotate("text", label="b", x=3, y=100, size = 5)  +
      annotate("text", label="b", x=4, y=100, size = 5)  +
      annotate("text", label="a", x=5, y=100, size = 5)  +
  theme(legend.position="none") +
  labs(caption = "Médias seguidas de mesma letra indicam diferença nula à 5%")

## Warning: Ignoring unknown parameters: with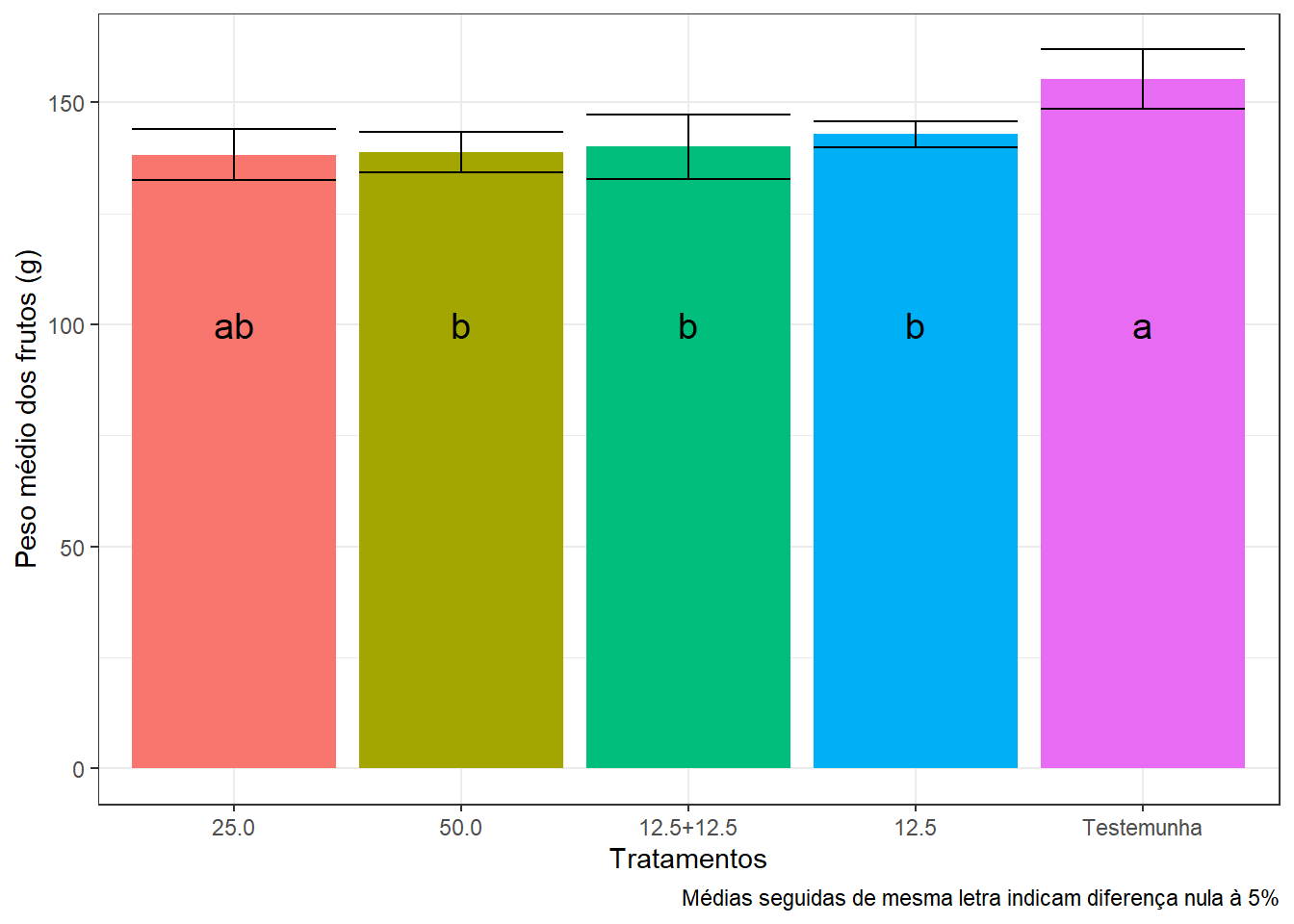

8.2.3 Teste não parametrico

As funções para comparações multiplas não-paramétricas incluídas no pacote agricolae são: kruskal, waerden.test, friedman, durbin.test e Conover (1999). Os testes não-paramétricos post hoc (kruskal, friedman, durbin e waerden) estão usando o critério da diferença menos significativa de Fisher (LSD).

Carregar pacote:

library(agricolae)

A função kruskal é usada para N amostras (N> 2), populações ou dados provenientes de um experimento aleatório (populações = tratamentos):

woutKruskal<-with(dados,kruskal(promalin, y = peso
  ,p.adj="bon",group=T, console=T))

## 
## Study: peso ~ promalin
## Kruskal-Wallis test's
## Ties or no Ties
## 
## Critical Value: 10.41429
## Degrees of freedom: 4
## Pvalue Chisq  : 0.03399839 
## 
## promalin,  means of the ranks
## 
##             peso r
## 12.5       12.00 4
## 12.5+12.5   7.75 4
## 25.0        7.50 4
## 50.0        7.00 4
## Testemunha 18.25 4
## 
## Post Hoc Analysis
## 
## P value adjustment method: bonferroni
## t-Student: 3.286039
## Alpha    : 0.05
## Minimum Significant Difference: 10.40002 
## 
## Treatments with the same letter are not significantly different.
## 
##             peso groups
## Testemunha 18.25      a
## 12.5       12.00     ab
## 12.5+12.5   7.75      b
## 25.0        7.50      b
## 50.0        7.00      b

print(woutKruskal$group)

##             peso groups
## Testemunha 18.25      a
## 12.5       12.00     ab
## 12.5+12.5   7.75      b
## 25.0        7.50      b
## 50.0        7.00      b

Gráficos:

par(mfrow=c(2,2),mar=c(3,3,1,1),cex=0.8)
bar.group(woutKruskal$group,ylim=c(0,100), xlab ="promalin")
bar.group(woutKruskal$group,xlim=c(0,100),horiz = TRUE)
plot(woutKruskal)
plot(woutKruskal,variation="IQR",horiz = TRUE)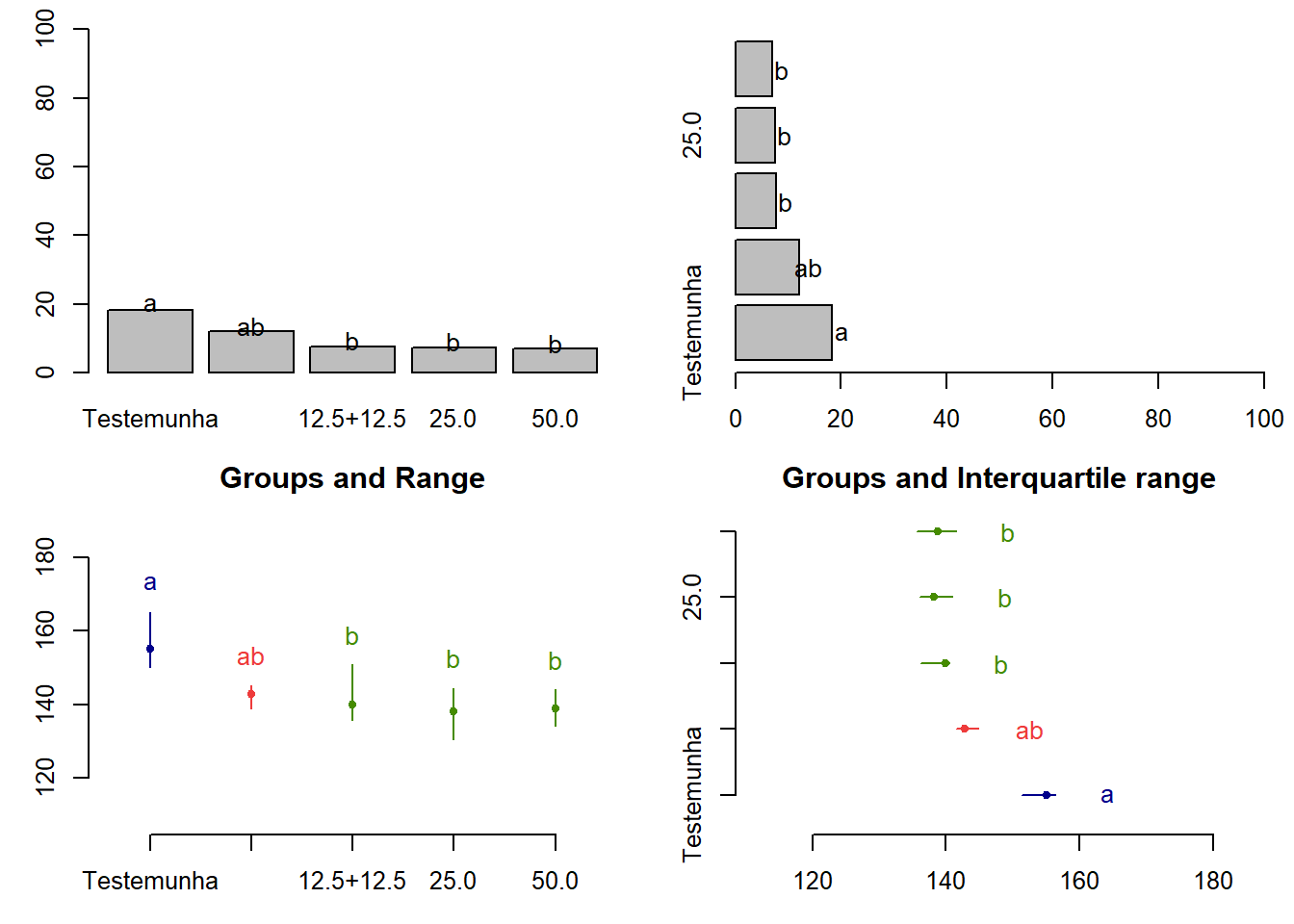

A função friedman é usada para análise de tratamentos do estudo randomizado de bloco completo, onde a resposta não pode ser tratada através da análise de variância:

woutfriedman <- out<-with(dados,friedman(bloco,promalin, peso,alpha=0.05, group=T,
  console=TRUE))

## 
## Study: peso ~ bloco + promalin 
## 
## promalin,  Sum of the ranks
## 
##            peso r
## 12.5          8 4
## 12.5+12.5     8 4
## 25.0         10 4
## 50.0         14 4
## Testemunha   20 4
## 
## Friedman's Test
## ===============
## Adjusted for ties
## Critical Value: 10.4
## P.Value Chisq: 0.0342027
## F Value: 5.571429
## P.Value F: 0.009007502 
## 
## Post Hoc Analysis
## 
## Alpha: 0.05 ; DF Error: 12
## t-Student: 2.178813
## LSD: 6.656383 
## 
## Treatments with the same letter are not significantly different.
## 
##            Sum of ranks groups
## Testemunha           20      a
## 50.0                 14     ab
## 25.0                 10      b
## 12.5                  8      b
## 12.5+12.5             8      b

Gráfico:

par(mfrow=c(2,2),mar=c(3,3,1,1),cex=0.8)
bar.group(woutfriedman$group,ylim=c(0,100), xlab ="promalin")
bar.group(woutfriedman$group,xlim=c(0,100),horiz = TRUE)
plot(woutfriedman)
plot(woutfriedman,variation="IQR",horiz = TRUE)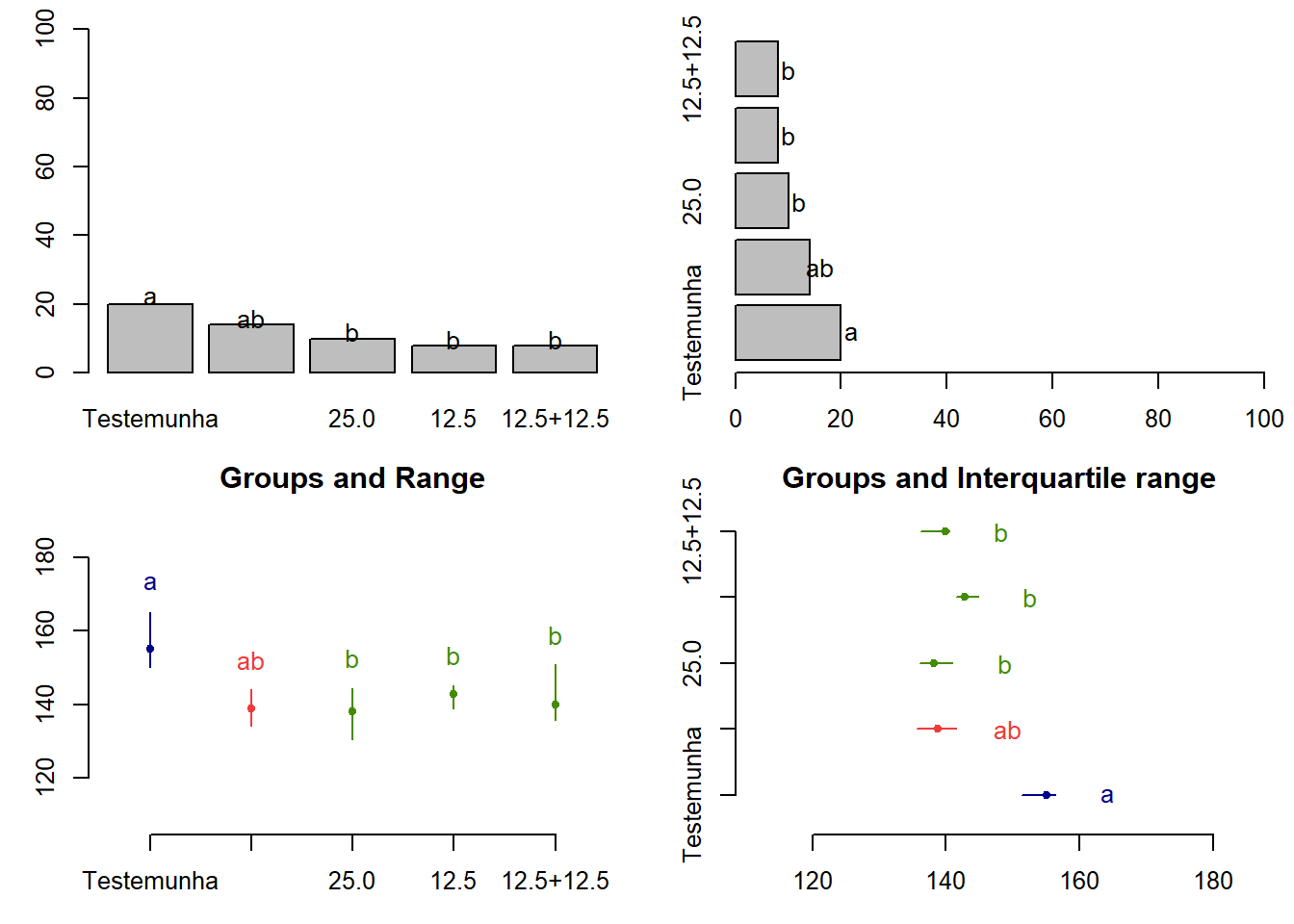

8.2.4 Exercicio 1

Obtenha: Análise exploratória, Análise de variância, teste de comparação múltipla, e recomendações.

Comparação de métodos de Semeadura do Mamoeiro

Estudo realizado em Jaboticabal - SP por Ruiz (1977) que comparou métodos de semeadura no mamoeiro. O experimento foi instalado em delineamento de blocos casualizados, com 4 repetições, avaliando 3 métodos de semeadura. Foram avaliadas duas unidades experimentais por método em cada bloco.

Importando dados:

dados <- read.table("https://www.dropbox.com/s/40m95attfw2fdh2/BanzattoQd4.7.1.txt?dl=1")

Conferir se temos fatores para fazer a análise de variância:

str(dados)

## 'data.frame':    24 obs. of  3 variables:
##  $ bloco : Factor w/ 4 levels "I","II","III",..: 1 1 2 2 3 3 4 4 1 1 ...
##  $ semead: Factor w/ 3 levels "Direta no campo",..: 1 1 1 1 1 1 1 1 2 2 ...
##  $ altura: num  136.1 105.3 98.8 86.8 108.8 ...

Gráficos:

addmargins(with(dados,
  tapply(X = altura,
    INDEX = list(semead, bloco),
    FUN = sum)))

##                     I    II   III    IV    Sum
## Direta no campo 241.4 185.6 218.5 162.9  808.4
## Recip. ao sol   157.7 120.7 129.0  80.1  487.5
## Recip. ripado   123.5 127.1 132.9 109.8  493.3
## Sum             522.6 433.4 480.4 352.8 1789.2

xyplot(altura ~ semead, data = dados,
  groups = bloco, type = c("p", "a"),
  xlab = "Método de semeadura de mamoeiro",
  ylab = "Altura média de planta de mamoeiro aos 147 DAS (cm)",
  auto.key = list(title = "Bloco", cex.title = 1, columns = 2))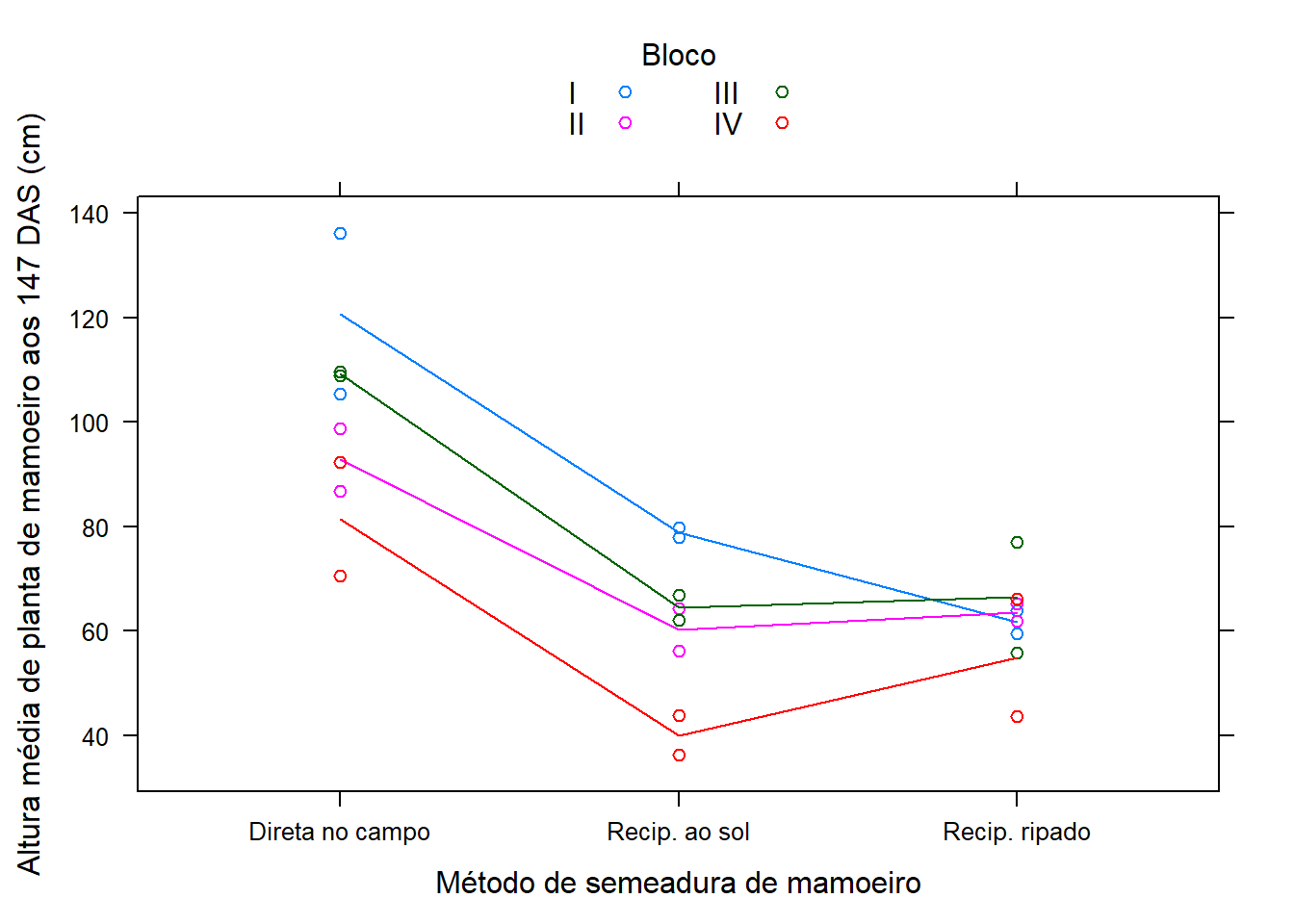

Análise de Variância:

m0 <- aov(altura~bloco+semead, data=dados)
class(m0)

## [1] "aov" "lm"

anova(m0)

## Analysis of Variance Table
## 
## Response: altura
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## bloco      3 2648.2   882.7  7.2162  0.002219 ** 
## semead     2 8429.1  4214.6 34.4535 7.014e-07 ***
## Residuals 18 2201.9   122.3                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

summary(m0)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## bloco        3   2648     883   7.216  0.00222 ** 
## semead       2   8429    4215  34.453 7.01e-07 ***
## Residuals   18   2202     122                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Checagem gráfica:

par(mfrow=c(2,2))
plot(m0)

layout(1)

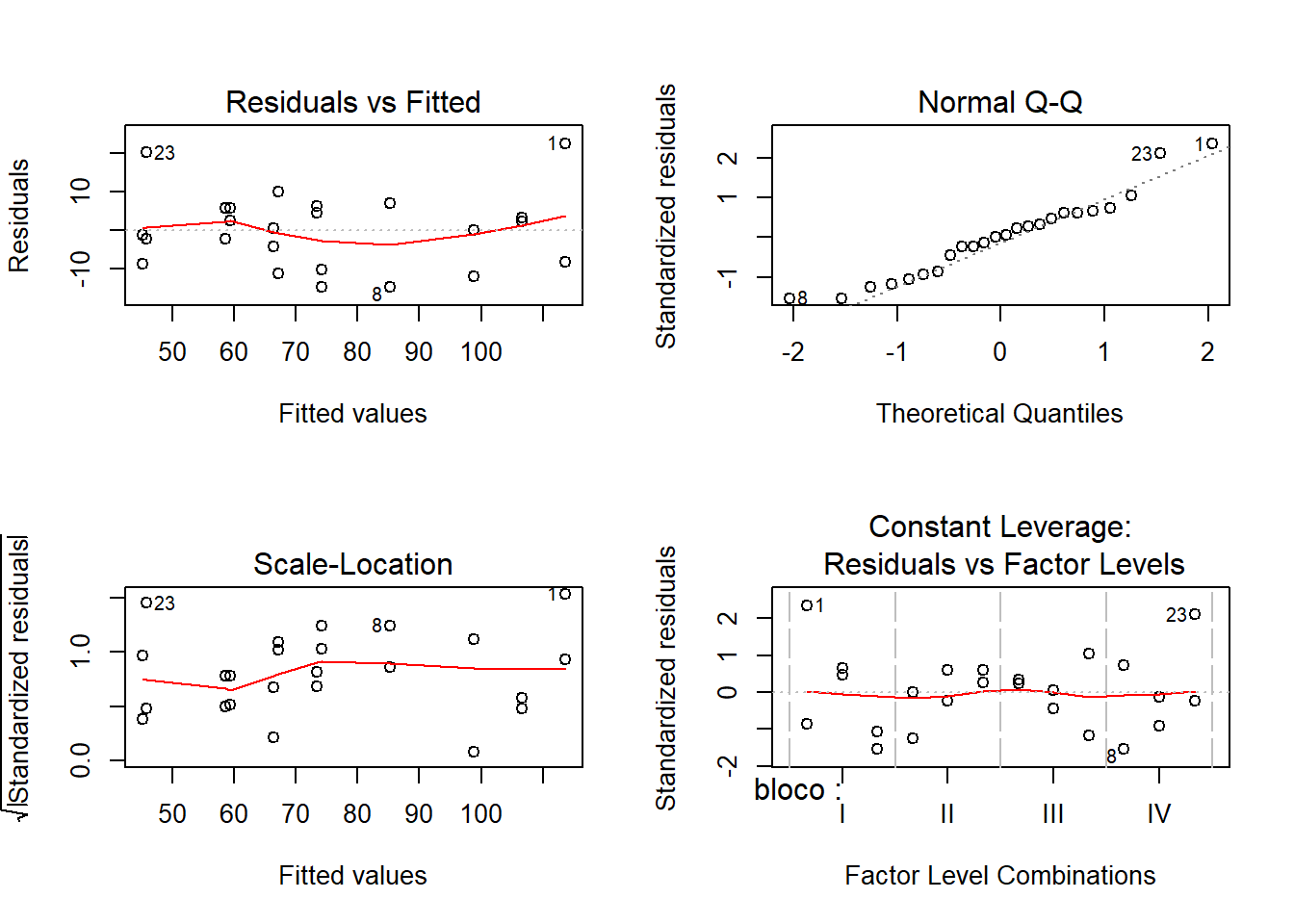
Teste das pressuposições de normalidade de homocedasticidade:

shapiro.test(residuals(m0))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(m0)
## W = 0.95197, p-value = 0.2988

bartlett.test(residuals(m0)~dados$semead)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  residuals(m0) by dados$semead
## Bartlett's K-squared = 4.5219, df = 2, p-value = 0.1043

Teste de médias

Teste de Tukey

require(agricolae)

tu <- with(dados, HSD.test(altura, semead,
DFerror=df.residual(m0),
MSerror=deviance(m0)/df.residual(m0)))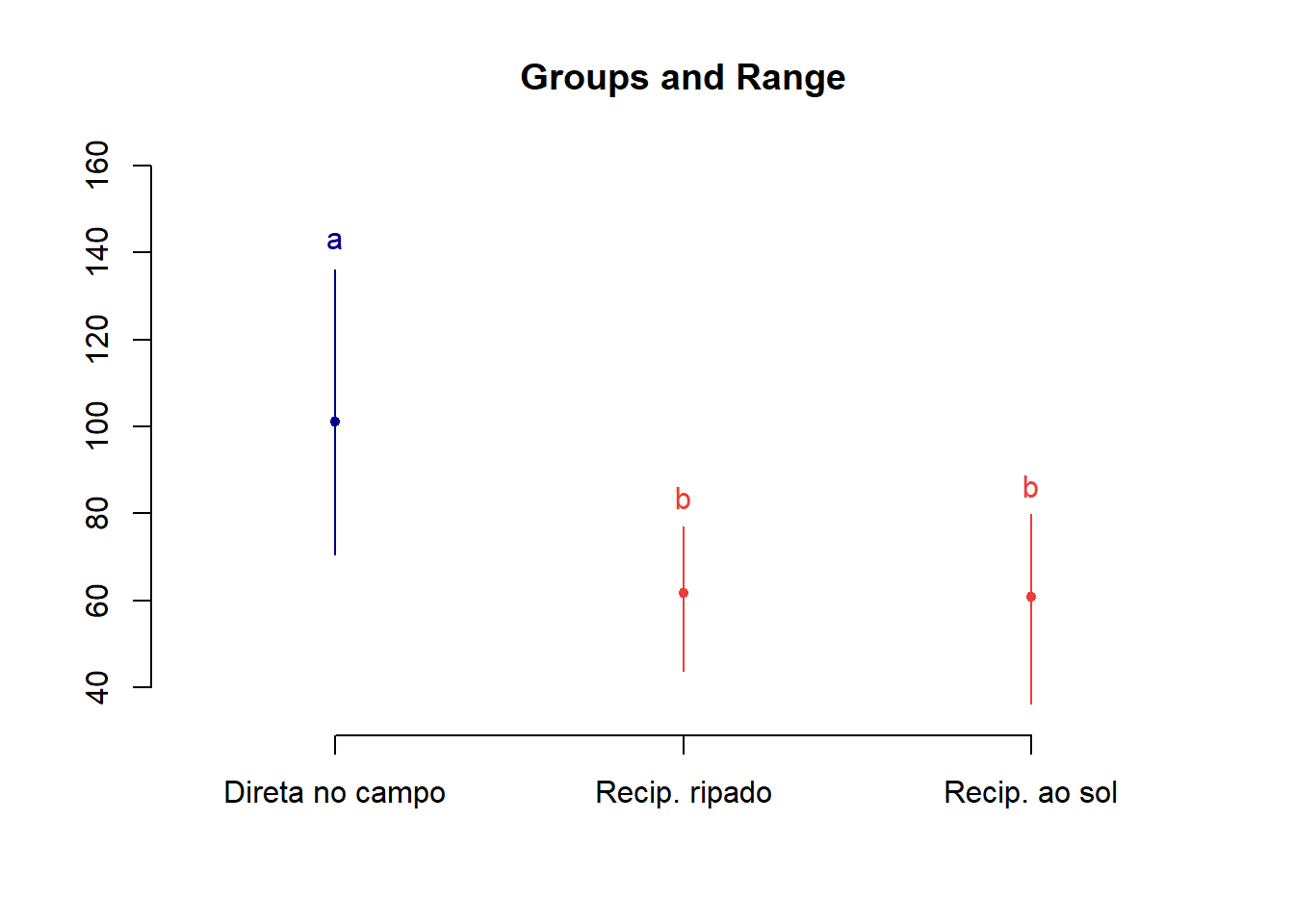

plot(tu)

print(tu)

## $statistics
##    MSerror Df  Mean       CV      MSD
##   122.3258 18 74.55 14.83581 14.11359
## 
## $parameters
##    test name.t ntr StudentizedRange alpha
##   Tukey semead   3         3.609304  0.05
## 
## $means
##                   altura       std r  Min   Max    Q25    Q50     Q75
## Direta no campo 101.0500 19.263956 8 70.5 136.1 91.000 102.05 109.025
## Recip. ao sol    60.9375 15.187489 8 36.3  79.8 53.175  63.25  69.650
## Recip. ripado    61.6625  9.544922 8 43.7  77.1 58.575  62.95  65.425
## 
## $comparison
## NULL
## 
## $groups
##                   altura groups
## Direta no campo 101.0500      a
## Recip. ripado    61.6625      b
## Recip. ao sol    60.9375      b
## 
## attr(,"class")
## [1] "group"

require(dplyr)
require(ggplot2)
  erro = summarise(group_by(dados, semead), 
    avg = mean(altura), sd = sd(altura))

  
  ggplot(erro, aes(semead, avg, fill=semead))+
    geom_bar(stat="identity")+
    geom_errorbar(aes(ymin=avg-sd, ymax =avg+sd), with=0.1, col="black") +
    xlab("Tratamentos") + 
    ylab("Altura média de planta de mamoeiro aos 147 DAS (cm)") + 
    theme_bw() + 
    theme(legend.position="top") +
    annotate("text", label=tu$groups$groups[1], x=1, y=20, size = 5)  +
    annotate("text", label=tu$groups$groups[2], x=2, y=20, size = 5)  +
    annotate("text", label=tu$groups$groups[3], x=3, y=20, size = 5)  +
    
    theme(legend.position="none") +
    labs(caption = "Médias seguidas de mesma letra indicam diferença nula à 5%")

## Warning: Ignoring unknown parameters: with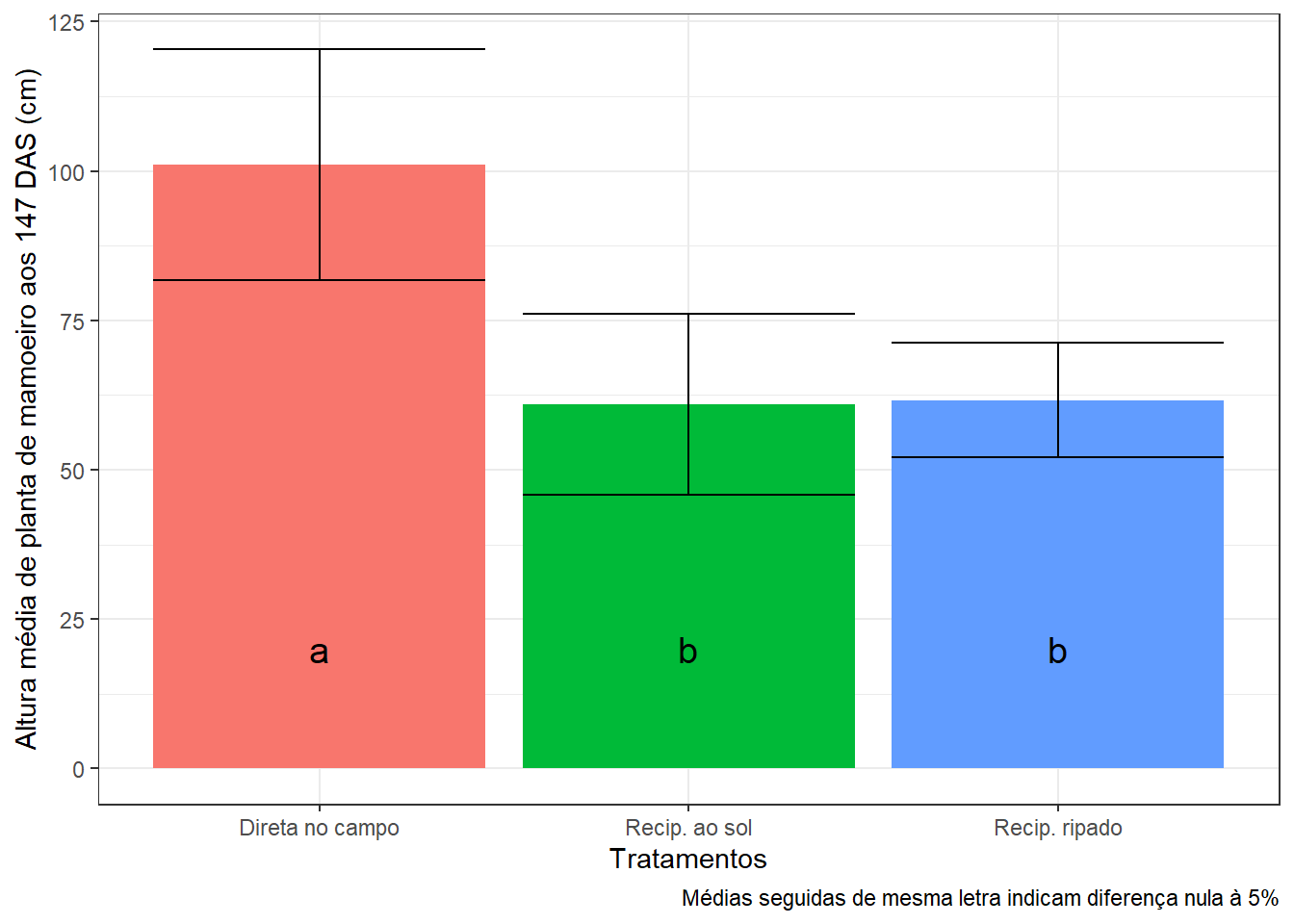

Teste de Scott-Knott

  library(ScottKnott)
  sk <- SK(x=dados, y=dados$altura, model="altura~bloco+semead", which="semead")
  summary(sk)

##           Levels    Means SK(5%)
##  Direta no campo 101.0500      a
##    Recip. ripado  61.6625      b
##    Recip. ao sol  60.9375      b

print(sk)

## $av
## Call:
##    aov(formula = altura ~ bloco + semead, data = dat)
## 
## Terms:
##                    bloco   semead Residuals
## Sum of Squares  2648.193 8429.103  2201.864
## Deg. of Freedom        3        2        18
## 
## Residual standard error: 11.0601
## Estimated effects may be unbalanced
## 
## $groups
## [1] 1 2 2
## 
## $nms
## [1] "Direta no campo" "Recip. ao sol"   "Recip. ripado"  
## 
## $ord
## [1] 1 3 2
## 
## $m.inf
##                     mean  min   max
## Direta no campo 101.0500 70.5 136.1
## Recip. ripado    61.6625 43.7  77.1
## Recip. ao sol    60.9375 36.3  79.8
## 
## $sig.level
## [1] 0.05
## 
## attr(,"class")
## [1] "SK"   "list"

8.2.5 Referência

MELO, M. P.; PETERNELI, L. A. Conhecendo o R: Um visão mais que estatística. Viçosa, MG: UFV, 2013. 222p. Cap. 1.

BANZATTO, D. A; KRONKA, S. N. Experimentação agrícola. Jaboticabal, SP: FUNEP, 2006, 237p.

ZEVIANI, W. M. Estatística Básica e Experimentação no R. 45p.

Site: http://www.leg.ufpr.br/~paulojus/

8.3 Quadrado Latino

Esse material foi baseado nas aulas do Prof. Walmes Zeviani.

8.3.1 Banco de dados

Iremos instalar o pacote com banco de dados.

O labestData é um pacote para o software R de computação estatística que possui centenas de conjuntos de dados para o ensino e aprendizado de estatística. O pacote é desenvolvido pelo PET Estatística UFPR e conta com a participação de professores e colaboradores. O nome labest vem de LABoratório de ESTatística, que é o ambiente onde acontecem as aulas práticas do Curso de Estatística na UFPR.

library(devtools)

## Loading required package: usethis

Instalação do repositório de desenvolvimento no GitLab:

install_git(url = "https://gitlab.c3sl.ufpr.br/pet-estatistica/labestData.git",
            branch = "master", build_vignettes = TRUE)

Do repositório de divulgação no GitHub:

install_github(repo = "labestData",
               username = "pet-estatistica",
               ref = "master", build_vignettes = TRUE)

Instalação por Arquivos Compactados:

install.packages("http://leg.ufpr.br/~walmes/pacotes/labestData_0.1.17.458.zip",
  repos = NULL)

Lendo arquivos de dados:

Escolhendo os dados:

labestDataView()

###Escolher o banco de dados

PimentelEg6.2

##    linha coluna varied prod
## 1      1      1      D  432
## 2      2      1      C  724
## 3      3      1      E  489
## 4      4      1      B  494
## 5      5      1      A  515
## 6      1      2      A  518
## 7      2      2      E  478
## 8      3      2      B  384
## 9      4      2      D  500
## 10     5      2      C  660
## 11     1      3      B  458
## 12     2      3      A  524
## 13     3      3      C  556
## 14     4      3      E  313
## 15     5      3      D  438
## 16     1      4      C  583
## 17     2      4      B  550
## 18     3      4      D  297
## 19     4      4      A  486
## 20     5      4      E  394
## 21     1      5      E  331
## 22     2      5      D  400
## 23     3      5      A  420
## 24     4      5      C  501
## 25     5      5      B  318

help("PimentelEg6.2")

Experimento de competição de variedades de cana-de-açúcar no qual foram usadas cinco variedades dispostas em um delineamento quadrado latino 5 times 5. Converte para nome de objeto mais simples:

pim <- PimentelEg6.2 
help(pim)

## No documentation for 'pim' in specified packages and libraries:
## you could try '??pim'

Verificar estrutura dos dados

str(pim)

## 'data.frame':    25 obs. of  4 variables:
##  $ linha : Factor w/ 5 levels "1","2","3","4",..: 1 2 3 4 5 1 2 3 4 5 ...
##  $ coluna: Factor w/ 5 levels "1","2","3","4",..: 1 1 1 1 1 2 2 2 2 2 ...
##  $ varied: Factor w/ 5 levels "A","B","C","D",..: 4 3 5 2 1 1 5 2 4 3 ...
##  $ prod  : int  432 724 489 494 515 518 478 384 500 660 ...

Vendo o quadrado no plano:

require(reshape)

## Loading required package: reshape

## 
## Attaching package: 'reshape'

## The following object is masked from 'package:dplyr':
## 
##     rename

## The following objects are masked from 'package:plyr':
## 
##     rename, round_any

Pacote gráfico:

require(latticeExtra)

## Loading required package: latticeExtra

## 
## Attaching package: 'latticeExtra'

## The following object is masked from 'package:ggplot2':
## 
##     layer

Gerar gráfico:

levelplot(prod~linha+coluna, data=pim, aspect="iso") + 
  layer(with(pim, panel.text(x=linha, y=coluna, label=paste(varied, prod))))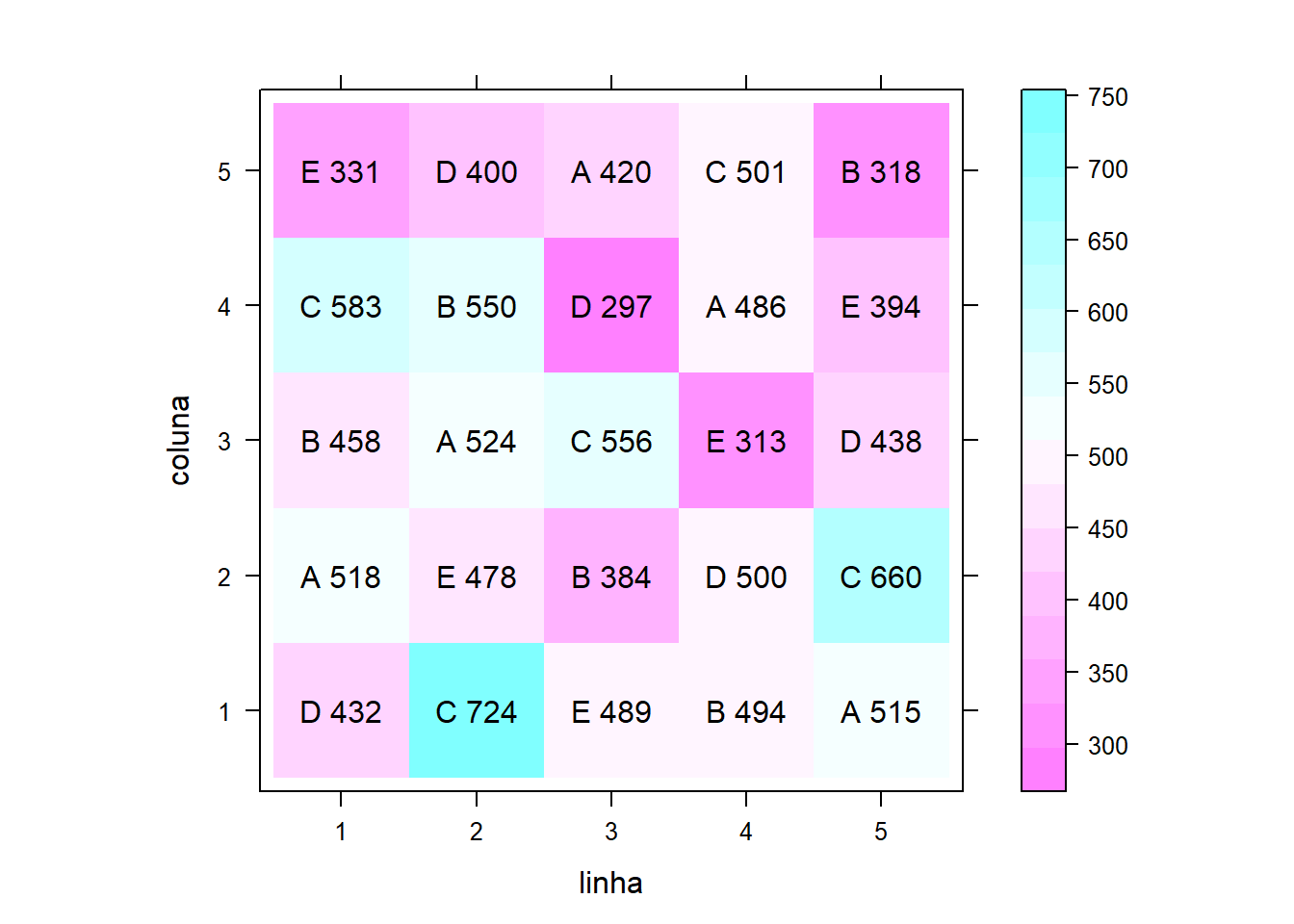

ANOVA:

m0 = lm (prod ~linha + coluna + varied, data = pim)

Pressuposto seja atendidos?

par(mfrow = c(2,2)) 
plot(m0)

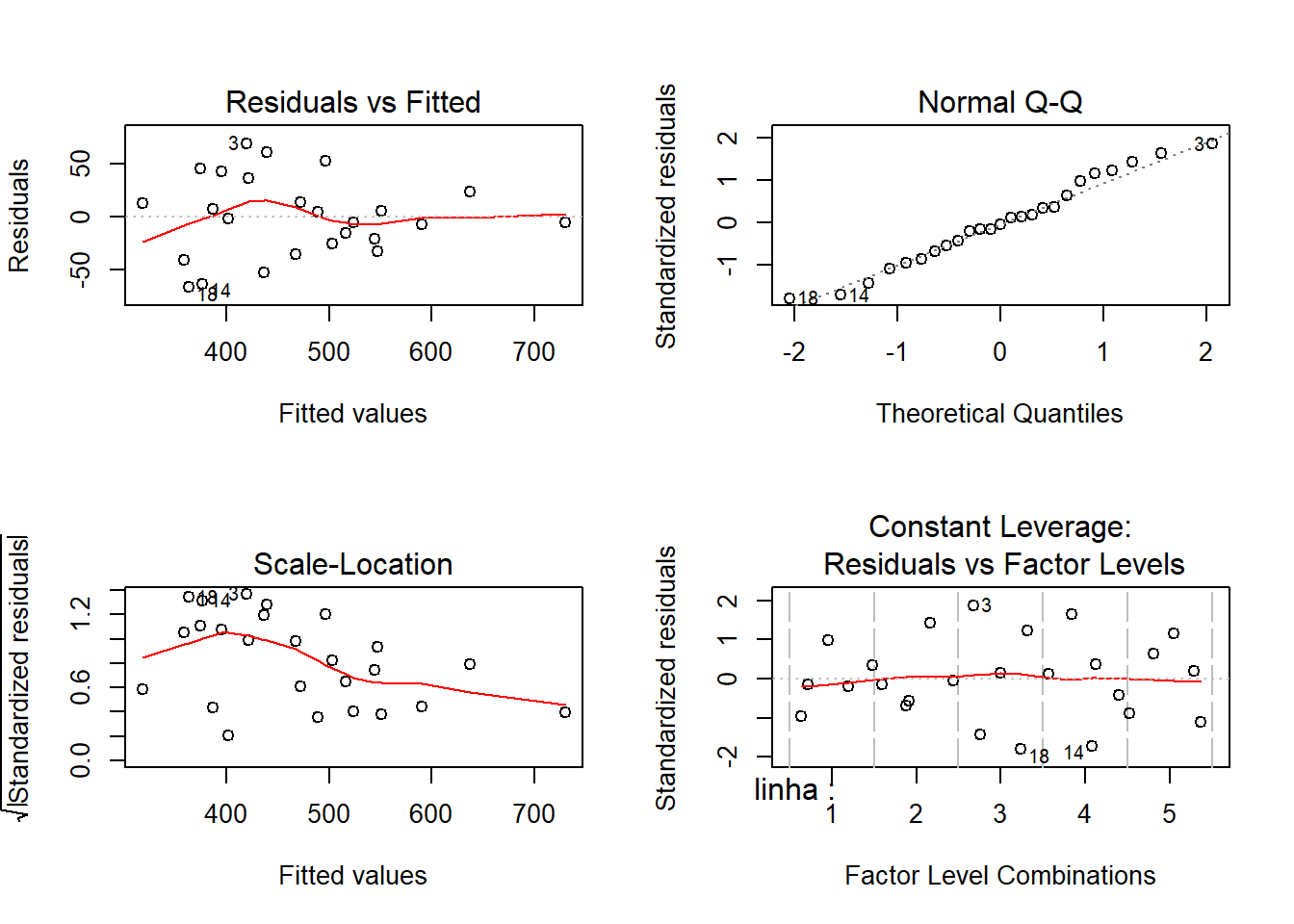
Teste de Bartllet para homocedasticidade:

bartlett.test(m0$residuals ~ pim$varied)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  m0$residuals by pim$varied
## Bartlett's K-squared = 5.6629, df = 4, p-value = 0.2258

Teste de Shapiro-Wilk para Normalidade:

shapiro.test(m0$res)

## 
##  Shapiro-Wilk normality test
## 
## data:  m0$res
## W = 0.97701, p-value = 0.8202

Quadro de análise de variância:

anova(m0)

## Analysis of Variance Table
## 
## Response: prod
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## linha      4  30481    7620  2.6804 0.0831343 .  
## coluna     4  55641   13910  4.8930 0.0142293 *  
## varied     4 137488   34372 12.0905 0.0003585 ***
## Residuals 12  34115    2843                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

summary(m0)

## 
## Call:
## lm(formula = prod ~ linha + coluna + varied, data = pim)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -66.56 -25.16  -1.56  23.24  69.04 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   546.76      38.45  14.220 7.14e-09 ***
## linha2         70.80      33.72   2.100  0.05759 .  
## linha3        -35.20      33.72  -1.044  0.31713    
## linha4         -5.60      33.72  -0.166  0.87087    
## linha5          0.60      33.72   0.018  0.98610    
## coluna2       -22.80      33.72  -0.676  0.51178    
## coluna3       -73.00      33.72  -2.165  0.05127 .  
## coluna4       -68.80      33.72  -2.040  0.06397 .  
## coluna5      -136.80      33.72  -4.057  0.00159 ** 
## variedB       -51.80      33.72  -1.536  0.15045    
## variedC       112.20      33.72   3.327  0.00603 ** 
## variedD       -79.20      33.72  -2.349  0.03680 *  
## variedE       -91.60      33.72  -2.716  0.01873 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 53.32 on 12 degrees of freedom
## Multiple R-squared:  0.8676, Adjusted R-squared:  0.7353 
## F-statistic: 6.555 on 12 and 12 DF,  p-value: 0.001366

Teste de média de comparações múltiplas:

library(doBy) # obter as médias ajustadas 
library(multcomp)
p0 = LSmeans(m0, effect = "varied", level = 0.95)

Verificar estrutura:

str(p0)

## List of 3
##  $ coef:'data.frame':    5 obs. of  5 variables:
##   ..$ estimate : num [1:5] 493 441 605 413 401
##   ..$ std.error: num [1:5] 23.8 23.8 23.8 23.8 23.8
##   ..$ statistic: num [1:5] 20.7 18.5 25.4 17.3 16.8
##   ..$ df       : num [1:5] 12 12 12 12 12
##   ..$ p.value  : num [1:5] 9.55e-11 3.49e-10 8.57e-12 7.34e-10 1.04e-09
##  $ grid:'data.frame':    5 obs. of  1 variable:
##   ..$ varied: chr [1:5] "A" "B" "C" "D" ...
##  $ L   : 'linest_matrix_class' num [1:5, 1:13] 1 1 1 1 1 0.2 0.2 0.2 0.2 0.2 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##   ..- attr(*, "grid")='data.frame':  5 obs. of  1 variable:
##   .. ..$ varied: chr [1:5] "A" "B" "C" "D" ...
##  - attr(*, "class")= chr "linest_class"

p0

## Coefficients:
##      estimate std.error statistic      df p.value
## [1,]  492.600    23.845    20.659  12.000       0
## [2,]  440.800    23.845    18.486  12.000       0
## [3,]  604.800    23.845    25.364  12.000       0
## [4,]  413.400    23.845    17.337  12.000       0
## [5,]  401.000    23.845    16.817  12.000       0

library(devtools) 
install_github("walmes/wzRfun", ref = "master")

## Using github PAT from envvar GITHUB_PAT

## Skipping install of 'wzRfun' from a github remote, the SHA1 (a90b379a) has not changed since last install.
##   Use `force = TRUE` to force installation

require(wzRfun)

## Loading required package: wzRfun

## ----------------------------------------------------------------------
##   wzRfun: Walmes Zeviani's collection of functions
## 
##   wzRfun (0.91, built on 2019-07-11) was loaded.
##   Consult online documentation at:
##     http://leg.ufpr.br/~walmes/pacotes/wzRfun
##   For collaboration, support or bug report, visit:
##     https://github.com/walmes/wzRfun/issues
##   For general information: packageDescription("wzRfun")
##   To access the package documentation: help(package = "wzRfun")
## ----------------------------------------------------------------------

Comparações múltiplas, contrastes de Tukey. Método de correção de p-valor: single-step

tu <- summary(glht(m0, linfct=mcp(varied="Tukey"))) 
tu

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lm(formula = prod ~ linha + coluna + varied, data = pim)
## 
## Linear Hypotheses:
##            Estimate Std. Error t value Pr(>|t|)    
## B - A == 0   -51.80      33.72  -1.536  0.56046    
## C - A == 0   112.20      33.72   3.327  0.03944 *  
## D - A == 0   -79.20      33.72  -2.349  0.19553    
## E - A == 0   -91.60      33.72  -2.716  0.10970    
## C - B == 0   164.00      33.72   4.863  0.00293 ** 
## D - B == 0   -27.40      33.72  -0.813  0.92177    
## E - B == 0   -39.80      33.72  -1.180  0.76211    
## D - C == 0  -191.40      33.72  -5.676  < 0.001 ***
## E - C == 0  -203.80      33.72  -6.044  < 0.001 ***
## E - D == 0   -12.40      33.72  -0.368  0.99556    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

Resumo compacto com letras:

cld(tu)

##   A   B   C   D   E 
## "a" "a" "b" "a" "a"

#cld(tu, decreasing=T)

Médias com intervalo de confiança:

ci <- confint(glht(m0, linfct= p0$L)) 
str(ci)

## List of 9
##  $ model      :List of 13
##   ..$ coefficients : Named num [1:13] 546.8 70.8 -35.2 -5.6 0.6 ...
##   .. ..- attr(*, "names")= chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##   ..$ residuals    : Named num [1:25] -35.56 -5.76 69.04 4.64 -32.36 ...
##   .. ..- attr(*, "names")= chr [1:25] "1" "2" "3" "4" ...
##   ..$ effects      : Named num [1:25] -2352.6 -161.7 64.937 10.772 -0.949 ...
##   .. ..- attr(*, "names")= chr [1:25] "(Intercept)" "linha2" "linha3" "linha4" ...
##   ..$ rank         : int 13
##   ..$ fitted.values: Named num [1:25] 468 730 420 489 547 ...
##   .. ..- attr(*, "names")= chr [1:25] "1" "2" "3" "4" ...
##   ..$ assign       : int [1:13] 0 1 1 1 1 2 2 2 2 3 ...
##   ..$ qr           :List of 5
##   .. ..$ qr   : num [1:25, 1:13] -5 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 ...
##   .. .. ..- attr(*, "dimnames")=List of 2
##   .. .. .. ..$ : chr [1:25] "1" "2" "3" "4" ...
##   .. .. .. ..$ : chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##   .. .. ..- attr(*, "assign")= int [1:13] 0 1 1 1 1 2 2 2 2 3 ...
##   .. .. ..- attr(*, "contrasts")=List of 3
##   .. .. .. ..$ linha : chr "contr.treatment"
##   .. .. .. ..$ coluna: chr "contr.treatment"
##   .. .. .. ..$ varied: chr "contr.treatment"
##   .. ..$ qraux: num [1:13] 1.2 1.42 1.41 1.4 1.38 ...
##   .. ..$ pivot: int [1:13] 1 2 3 4 5 6 7 8 9 10 ...
##   .. ..$ tol  : num 1e-07
##   .. ..$ rank : int 13
##   .. ..- attr(*, "class")= chr "qr"
##   ..$ df.residual  : int 12
##   ..$ contrasts    :List of 3
##   .. ..$ linha : chr "contr.treatment"
##   .. ..$ coluna: chr "contr.treatment"
##   .. ..$ varied: chr "contr.treatment"
##   ..$ xlevels      :List of 3
##   .. ..$ linha : chr [1:5] "1" "2" "3" "4" ...
##   .. ..$ coluna: chr [1:5] "1" "2" "3" "4" ...
##   .. ..$ varied: chr [1:5] "A" "B" "C" "D" ...
##   ..$ call         : language lm(formula = prod ~ linha + coluna + varied, data = pim)
##   ..$ terms        :Classes 'terms', 'formula'  language prod ~ linha + coluna + varied
##   .. .. ..- attr(*, "variables")= language list(prod, linha, coluna, varied)
##   .. .. ..- attr(*, "factors")= int [1:4, 1:3] 0 1 0 0 0 0 1 0 0 0 ...
##   .. .. .. ..- attr(*, "dimnames")=List of 2
##   .. .. .. .. ..$ : chr [1:4] "prod" "linha" "coluna" "varied"
##   .. .. .. .. ..$ : chr [1:3] "linha" "coluna" "varied"
##   .. .. ..- attr(*, "term.labels")= chr [1:3] "linha" "coluna" "varied"
##   .. .. ..- attr(*, "order")= int [1:3] 1 1 1
##   .. .. ..- attr(*, "intercept")= int 1
##   .. .. ..- attr(*, "response")= int 1
##   .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
##   .. .. ..- attr(*, "predvars")= language list(prod, linha, coluna, varied)
##   .. .. ..- attr(*, "dataClasses")= Named chr [1:4] "numeric" "factor" "factor" "factor"
##   .. .. .. ..- attr(*, "names")= chr [1:4] "prod" "linha" "coluna" "varied"
##   ..$ model        :'data.frame':    25 obs. of  4 variables:
##   .. ..$ prod  : int [1:25] 432 724 489 494 515 518 478 384 500 660 ...
##   .. ..$ linha : Factor w/ 5 levels "1","2","3","4",..: 1 2 3 4 5 1 2 3 4 5 ...
##   .. ..$ coluna: Factor w/ 5 levels "1","2","3","4",..: 1 1 1 1 1 2 2 2 2 2 ...
##   .. ..$ varied: Factor w/ 5 levels "A","B","C","D",..: 4 3 5 2 1 1 5 2 4 3 ...
##   .. ..- attr(*, "terms")=Classes 'terms', 'formula'  language prod ~ linha + coluna + varied
##   .. .. .. ..- attr(*, "variables")= language list(prod, linha, coluna, varied)
##   .. .. .. ..- attr(*, "factors")= int [1:4, 1:3] 0 1 0 0 0 0 1 0 0 0 ...
##   .. .. .. .. ..- attr(*, "dimnames")=List of 2
##   .. .. .. .. .. ..$ : chr [1:4] "prod" "linha" "coluna" "varied"
##   .. .. .. .. .. ..$ : chr [1:3] "linha" "coluna" "varied"
##   .. .. .. ..- attr(*, "term.labels")= chr [1:3] "linha" "coluna" "varied"
##   .. .. .. ..- attr(*, "order")= int [1:3] 1 1 1
##   .. .. .. ..- attr(*, "intercept")= int 1
##   .. .. .. ..- attr(*, "response")= int 1
##   .. .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
##   .. .. .. ..- attr(*, "predvars")= language list(prod, linha, coluna, varied)
##   .. .. .. ..- attr(*, "dataClasses")= Named chr [1:4] "numeric" "factor" "factor" "factor"
##   .. .. .. .. ..- attr(*, "names")= chr [1:4] "prod" "linha" "coluna" "varied"
##   ..- attr(*, "class")= chr "lm"
##  $ linfct     : 'linest_matrix_class' num [1:5, 1:13] 1 1 1 1 1 0.2 0.2 0.2 0.2 0.2 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:5] "1" "2" "3" "4" ...
##   .. ..$ : chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##   ..- attr(*, "grid")='data.frame':  5 obs. of  1 variable:
##   .. ..$ varied: chr [1:5] "A" "B" "C" "D" ...
##  $ rhs        : num [1:5] 0 0 0 0 0
##  $ coef       : Named num [1:13] 546.8 70.8 -35.2 -5.6 0.6 ...
##   ..- attr(*, "names")= chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##  $ vcov       : num [1:13, 1:13] 1478 -569 -569 -569 -569 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##   .. ..$ : chr [1:13] "(Intercept)" "linha2" "linha3" "linha4" ...
##  $ df         : int 12
##  $ alternative: chr "two.sided"
##  $ type       : NULL
##  $ confint    : num [1:5, 1:3] 493 441 605 413 401 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:5] "1" "2" "3" "4" ...
##   .. ..$ : chr [1:3] "Estimate" "lwr" "upr"
##   ..- attr(*, "conf.level")= num 0.95
##   ..- attr(*, "calpha")= num 3
##  - attr(*, "class")= chr [1:2] "confint.glht" "glht"
##  - attr(*, "type")= chr "adjusted"

Juntar com os nomes dos tratramentos com os intervalos:

ci <- cbind(p0$grid, ci$confint)

Colocar as letras. onde estão as letras?

str(cld(tu))

## List of 10
##  $ y        : int [1:25] 432 724 489 494 515 518 478 384 500 660 ...
##  $ yname    : chr "prod"
##  $ x        : Factor w/ 5 levels "A","B","C","D",..: 4 3 5 2 1 1 5 2 4 3 ...
##  $ xname    : chr "varied"
##  $ weights  : NULL
##  $ lp       : Named num [1:25] 468 730 420 489 547 ...
##   ..- attr(*, "names")= chr [1:25] "1" "2" "3" "4" ...
##  $ covar    : logi TRUE
##  $ comps    : chr [1:10, 1:2] "B" "C" "D" "E" ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:10] "B - A" "C - A" "D - A" "E - A" ...
##   .. ..$ : NULL
##  $ signif   : logi [1:10] FALSE TRUE FALSE FALSE TRUE FALSE ...
##  $ mcletters:List of 5
##   ..$ Letters          : Named chr [1:5] "a" "a" "b" "a" ...
##   .. ..- attr(*, "names")= chr [1:5] "A" "B" "C" "D" ...
##   ..$ monospacedLetters: Named chr [1:5] "a " "a " " b" "a " ...
##   .. ..- attr(*, "names")= chr [1:5] "A" "B" "C" "D" ...
##   ..$ LetterMatrix     : logi [1:5, 1:2] TRUE TRUE FALSE TRUE TRUE FALSE ...
##   .. ..- attr(*, "dimnames")=List of 2
##   .. .. ..$ : chr [1:5] "A" "B" "C" "D" ...
##   .. .. ..$ : chr [1:2] "a" "b"
##   ..$ aLetters         : chr [1:52] "a" "b" "c" "d" ...
##   ..$ aseparator       : chr "."
##   ..- attr(*, "class")= chr "multcompLetters"
##  - attr(*, "class")= chr "cld"

ci$cld <- cld(tu)$mcletters$Letters 
ci$cld

## [1] "a" "a" "b" "a" "a"

str(ci)

## 'data.frame':    5 obs. of  5 variables:
##  $ varied  : chr  "A" "B" "C" "D" ...
##  $ Estimate: num  493 441 605 413 401
##  $ lwr     : num  421 369 533 342 329
##  $ upr     : num  564 512 676 485 473
##  $ cld     : chr  "a" "a" "b" "a" ...

ci$varied <- factor(ci$varied)

Representação gráfica dos resultados:

require(latticeExtra) 
segplot(varied~lwr+upr, 
        centers=Estimate, 
        data=ci, 
        draw=F, #desenhar segmentos 
        xlab = expression("Tratamento"), 
        ylab = "Número de perfilhos", 
        sub = list("Médias seguidas de mesma letra indicam diferença nula à 5%.", 
                   font=1, cex=0.8)) + 
layer(panel.text( x = centers, 
                 y = z, 
                 labels = sprintf("%0.2f %s", centers, ci$cld), 
                 pos = 3))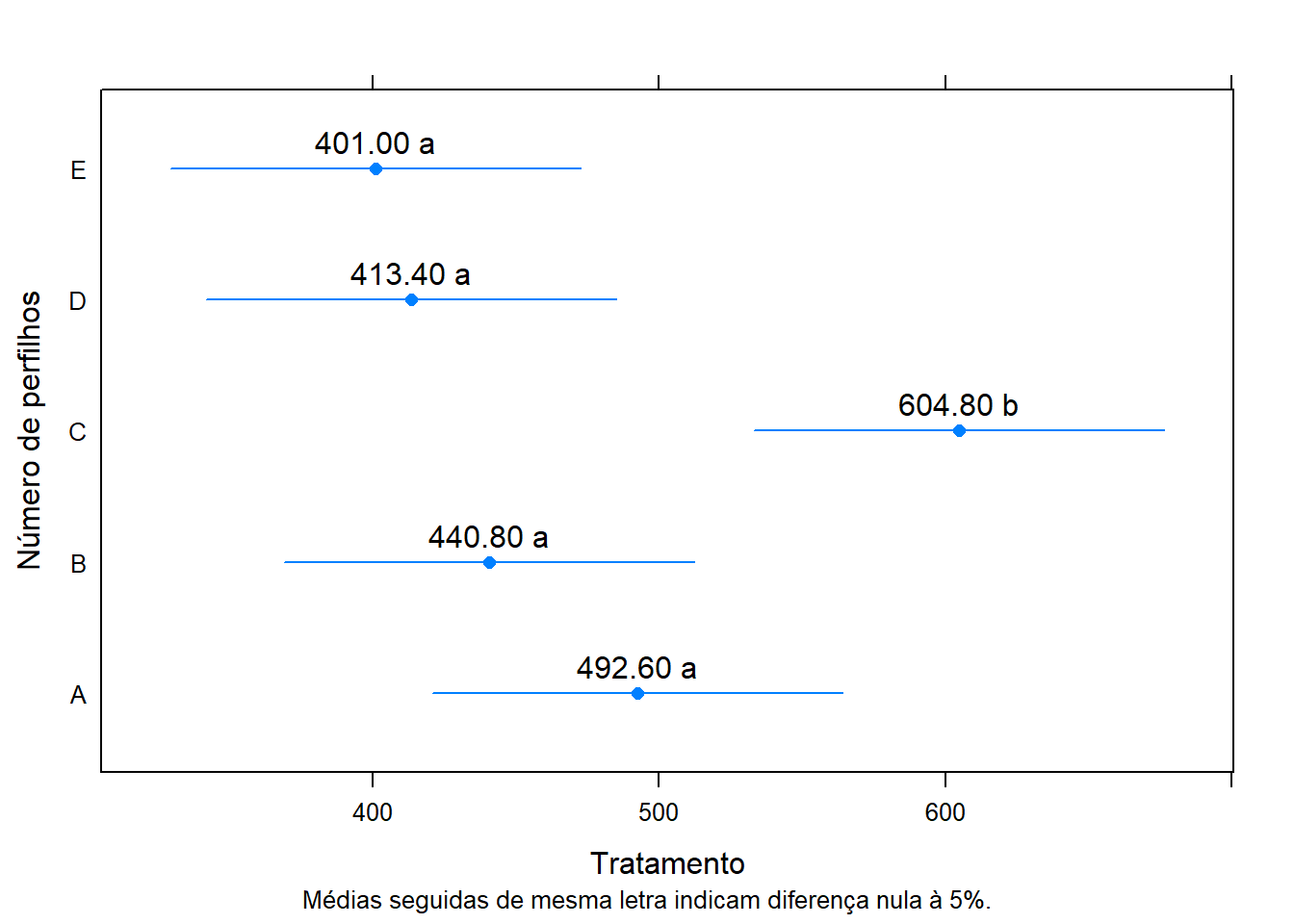

8.3.2 Exercicios

require(labestData)

ZimmermannTb5.15

##    linha coluna trat perf
## 1      1      1    1  155
## 2      2      1    5  198
## 3      3      1    4  187
## 4      4      1    2  204
## 5      5      1    6  209
## 6      6      1    3  216
## 7      1      2    5  191
## 8      2      2    3  199
## 9      3      2    2  213
## 10     4      2    6  225
## 11     5      2    4  218
## 12     6      2    1  181
## 13     1      3    6  203
## 14     2      3    4  205
## 15     3      3    3  195
## 16     4      3    1  135
## 17     5      3    5  196
## 18     6      3    2  178
## 19     1      4    3  187
## 20     2      4    1  186
## 21     3      4    6  177
## 22     4      4    4  190
## 23     5      4    2  209
## 24     6      4    5  215
## 25     1      5    2  162
## 26     2      5    6  181
## 27     3      5    5  188
## 28     4      5    3  204
## 29     5      5    1  175
## 30     6      5    4  203
## 31     1      6    4  167
## 32     2      6    2  174
## 33     3      6    1  161
## 34     4      6    5  181
## 35     5      6    3  210
## 36     6      6    6  206

help(ZimmermannTb5.15) 
str(ZimmermannTb5.15)

## 'data.frame':    36 obs. of  4 variables:
##  $ linha : Factor w/ 6 levels "1","2","3","4",..: 1 2 3 4 5 6 1 2 3 4 ...
##  $ coluna: Factor w/ 6 levels "1","2","3","4",..: 1 1 1 1 1 1 2 2 2 2 ...
##  $ trat  : Factor w/ 6 levels "1","2","3","4",..: 1 5 4 2 6 3 5 3 2 6 ...
##  $ perf  : num  155 198 187 204 209 216 191 199 213 225 ...

Atribuir um nome menor ao conjunto de dados:

dados <- ZimmermannTb5.15

Gráfico do layout:

require(latticeExtra) 

levelplot(perf~linha+coluna, 
          data=dados, aspect="iso")+ 
          layer(with(dados, 
          panel.text(x=linha, y=coluna, 
          label=paste(trat, perf))))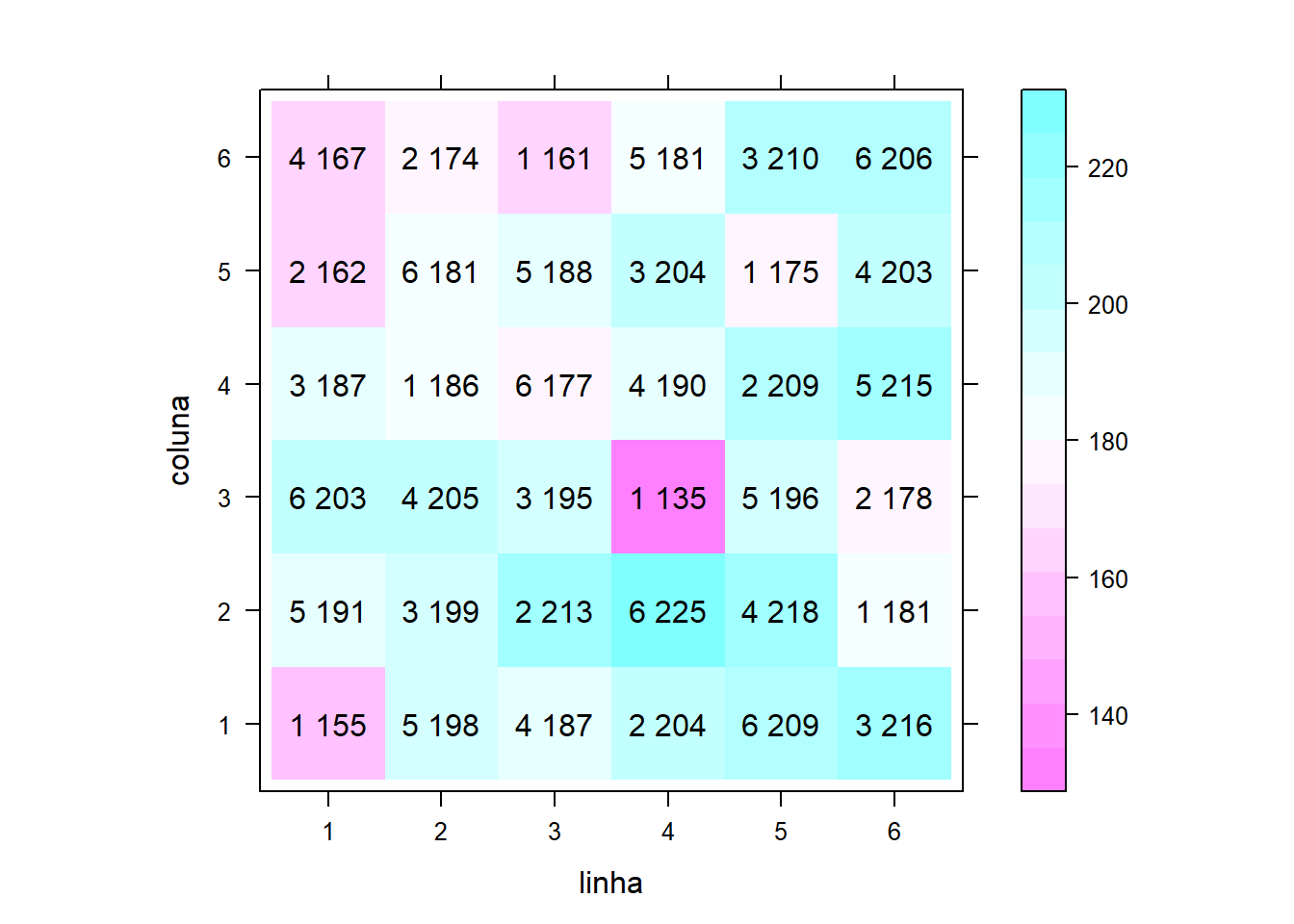

require(latticeExtra)

Gráfico do layout:

levelplot(perf~linha+coluna, 
          data=dados, aspect="iso")+ 
          layer(with(dados, 
          panel.text(x=linha, y=coluna, 
          label=paste(trat, perf))))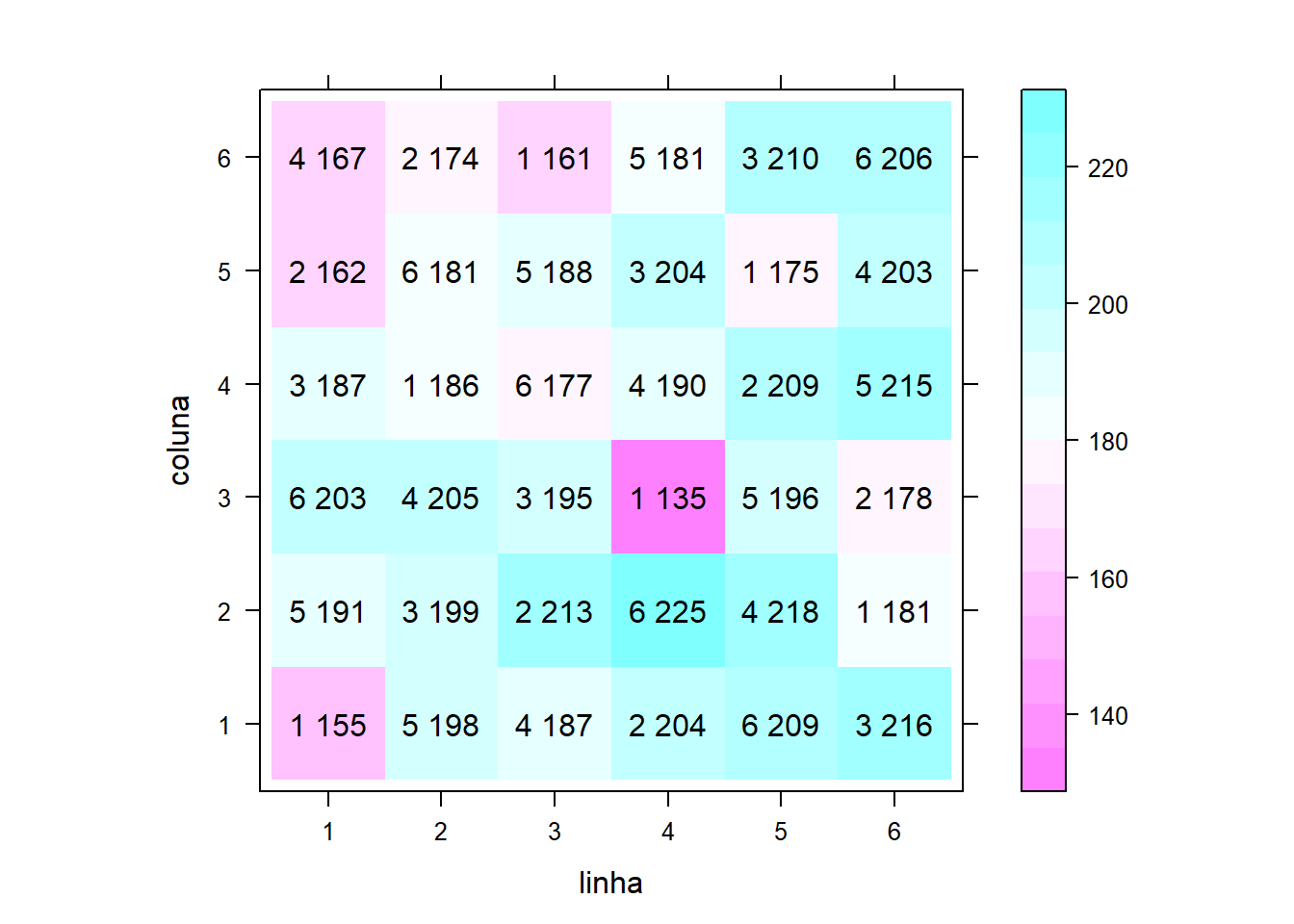

ANOVA:

m0 = lm (perf~linha + coluna + trat, data = dados)

Foram atendidos?

par(mfrow = c(2,2)) 
plot(m0)

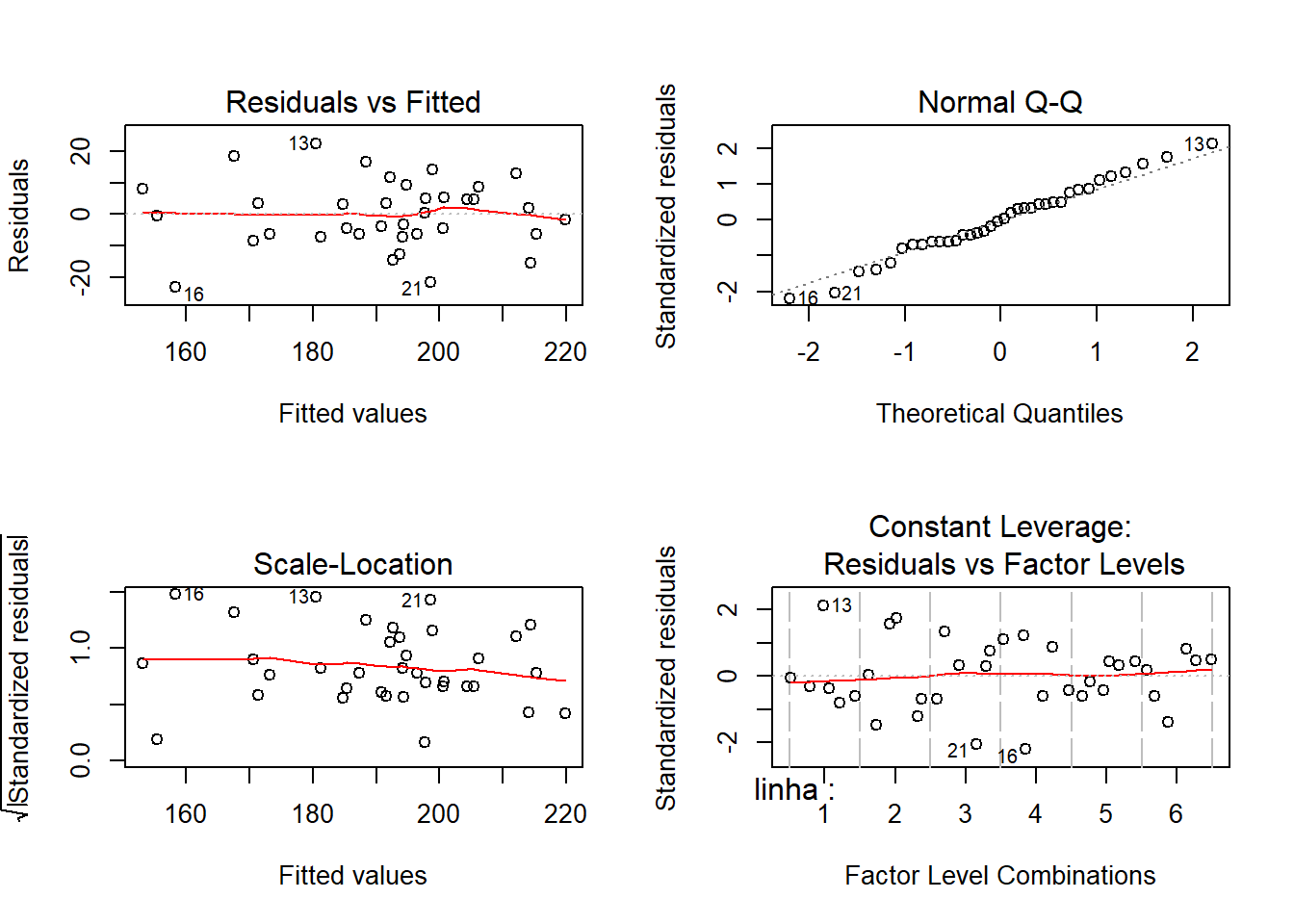
Teste de Bartllet para homocedasticidade:

bartlett.test(m0$res, dados$trat)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  m0$res and dados$trat
## Bartlett's K-squared = 6.5685, df = 5, p-value = 0.2548

Teste de Shapiro-Wilk para Normalidade:

shapiro.test(m0$res)

## 
##  Shapiro-Wilk normality test
## 
## data:  m0$res
## W = 0.98701, p-value = 0.9408

Quadro de análise de variância:

anova(m0)

## Analysis of Variance Table
## 
## Response: perf
##           Df Sum Sq Mean Sq F value  Pr(>F)   
## linha      5 2513.9  502.78  2.5039 0.06461 . 
## coluna     5 1976.2  395.24  1.9684 0.12760   
## trat       5 5298.2 1059.64  5.2773 0.00299 **
## Residuals 20 4015.9  200.79                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

summary(m0)

## 
## Call:
## lm(formula = perf ~ linha + coluna + trat, data = dados)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -23.2222  -6.3889  -0.0556   5.9444  22.4444 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 155.3889     9.4468  16.449 4.34e-13 ***
## linha2       13.0000     8.1812   1.589 0.127741    
## linha3        9.3333     8.1812   1.141 0.267417    
## linha4       12.3333     8.1812   1.508 0.147310    
## linha5       25.3333     8.1812   3.097 0.005689 ** 
## linha6       22.3333     8.1812   2.730 0.012905 *  
## coluna2       9.6667     8.1812   1.182 0.251234    
## coluna3      -9.5000     8.1812  -1.161 0.259231    
## coluna4      -0.8333     8.1812  -0.102 0.919882    
## coluna5      -9.3333     8.1812  -1.141 0.267417    
## coluna6     -11.6667     8.1812  -1.426 0.169280    
## trat2        24.5000     8.1812   2.995 0.007161 ** 
## trat3        36.3333     8.1812   4.441 0.000251 ***
## trat4        29.5000     8.1812   3.606 0.001764 ** 
## trat5        29.3333     8.1812   3.585 0.001850 ** 
## trat6        34.6667     8.1812   4.237 0.000404 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.17 on 20 degrees of freedom
## Multiple R-squared:  0.7091, Adjusted R-squared:  0.4909 
## F-statistic:  3.25 on 15 and 20 DF,  p-value: 0.007591

Comparações múltiplas:

library(doBy) 
library(multcomp) 

p0 = LSmeans(m0, effect = "trat", level = 0.95) 

str(p0)

## List of 3
##  $ coef:'data.frame':    6 obs. of  5 variables:
##   ..$ estimate : num [1:6] 165 190 202 195 195 ...
##   ..$ std.error: num [1:6] 5.78 5.78 5.78 5.78 5.78 ...
##   ..$ statistic: num [1:6] 28.6 32.8 34.9 33.7 33.7 ...
##   ..$ df       : num [1:6] 20 20 20 20 20 20
##   ..$ p.value  : num [1:6] 1.06e-17 7.10e-19 2.16e-19 4.26e-19 4.33e-19 ...
##  $ grid:'data.frame':    6 obs. of  1 variable:
##   ..$ trat: chr [1:6] "1" "2" "3" "4" ...
##  $ L   : 'linest_matrix_class' num [1:6, 1:16] 1 1 1 1 1 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:16] "(Intercept)" "linha2" "linha3" "linha4" ...
##   ..- attr(*, "grid")='data.frame':  6 obs. of  1 variable:
##   .. ..$ trat: chr [1:6] "1" "2" "3" "4" ...
##  - attr(*, "class")= chr "linest_class"

Criando a tabela com as estimativas:

library(devtools) 
#install_github("walmes/wzRfun", ref = "master") 
require(wzRfun)

Comparações múltiplas, contrastes de Tukey. Método de correção de p-valor: single-step.

tu <- summary(glht(m0, linfct=mcp(trat="Tukey"))) 
tu

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lm(formula = perf ~ linha + coluna + trat, data = dados)
## 
## Linear Hypotheses:
##            Estimate Std. Error t value Pr(>|t|)   
## 2 - 1 == 0  24.5000     8.1812   2.995  0.06758 . 
## 3 - 1 == 0  36.3333     8.1812   4.441  0.00305 **
## 4 - 1 == 0  29.5000     8.1812   3.606  0.01885 * 
## 5 - 1 == 0  29.3333     8.1812   3.585  0.01974 * 
## 6 - 1 == 0  34.6667     8.1812   4.237  0.00469 **
## 3 - 2 == 0  11.8333     8.1812   1.446  0.69980   
## 4 - 2 == 0   5.0000     8.1812   0.611  0.98894   
## 5 - 2 == 0   4.8333     8.1812   0.591  0.99051   
## 6 - 2 == 0  10.1667     8.1812   1.243  0.81102   
## 4 - 3 == 0  -6.8333     8.1812  -0.835  0.95717   
## 5 - 3 == 0  -7.0000     8.1812  -0.856  0.95271   
## 6 - 3 == 0  -1.6667     8.1812  -0.204  0.99994   
## 5 - 4 == 0  -0.1667     8.1812  -0.020  1.00000   
## 6 - 4 == 0   5.1667     8.1812   0.632  0.98718   
## 6 - 5 == 0   5.3333     8.1812   0.652  0.98523   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

Resumo compacto com letras:

cld(tu)

##    1    2    3    4    5    6 
##  "a" "ab"  "b"  "b"  "b"  "b"

#cld(tu, decreasing=T)

Médias com intervalo de confiança:

ci <- confint(glht(m0, linfct= p0$L)) 
ci

## 
##   Simultaneous Confidence Intervals
## 
## Fit: lm(formula = perf ~ linha + coluna + trat, data = dados)
## 
## Quantile = 2.8974
## 95% family-wise confidence level
##  
## 
## Linear Hypotheses:
##        Estimate lwr      upr     
## 1 == 0 165.5000 148.7386 182.2614
## 2 == 0 190.0000 173.2386 206.7614
## 3 == 0 201.8333 185.0719 218.5948
## 4 == 0 195.0000 178.2386 211.7614
## 5 == 0 194.8333 178.0719 211.5948
## 6 == 0 200.1667 183.4052 216.9281

Juntar com os nomes dos tratramentos com os intervalos:

ci <- cbind(p0$grid, ci$confint) 

ci$cld <- cld(tu)$mcletters$Letters 

str(cld(tu))

## List of 10
##  $ y        : num [1:36] 155 198 187 204 209 216 191 199 213 225 ...
##  $ yname    : chr "perf"
##  $ x        : Factor w/ 6 levels "1","2","3","4",..: 1 5 4 2 6 3 5 3 2 6 ...
##  $ xname    : chr "trat"
##  $ weights  : NULL
##  $ lp       : Named num [1:36] 155 198 194 192 215 ...
##   ..- attr(*, "names")= chr [1:36] "1" "2" "3" "4" ...
##  $ covar    : logi TRUE
##  $ comps    : chr [1:15, 1:2] "2" "3" "4" "5" ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:15] "2 - 1" "3 - 1" "4 - 1" "5 - 1" ...
##   .. ..$ : NULL
##  $ signif   : logi [1:15] FALSE TRUE TRUE TRUE TRUE FALSE ...
##  $ mcletters:List of 5
##   ..$ Letters          : Named chr [1:6] "a" "ab" "b" "b" ...
##   .. ..- attr(*, "names")= chr [1:6] "1" "2" "3" "4" ...
##   ..$ monospacedLetters: Named chr [1:6] "a " "ab" " b" " b" ...
##   .. ..- attr(*, "names")= chr [1:6] "1" "2" "3" "4" ...
##   ..$ LetterMatrix     : logi [1:6, 1:2] TRUE TRUE FALSE FALSE FALSE FALSE ...
##   .. ..- attr(*, "dimnames")=List of 2
##   .. .. ..$ : chr [1:6] "1" "2" "3" "4" ...
##   .. .. ..$ : chr [1:2] "a" "b"
##   ..$ aLetters         : chr [1:52] "a" "b" "c" "d" ...
##   ..$ aseparator       : chr "."
##   ..- attr(*, "class")= chr "multcompLetters"
##  - attr(*, "class")= chr "cld"

Representação gráfica dos resultados:

require(latticeExtra) 

segplot(trat~lwr+upr, 
        centers=Estimate, 
        data=ci, 
        draw=F,
        xlab = expression(" "), ylab = " ", 
        sub = list("Médias seguidas de mesma letra indicam diferença nula à 5%.",
        font=1, cex=0.8)) + 
        layer(panel.text( x = centers, 
        y = z, 
        labels = sprintf("%0.2f %s", centers, ci$cld), 
        pos = 3))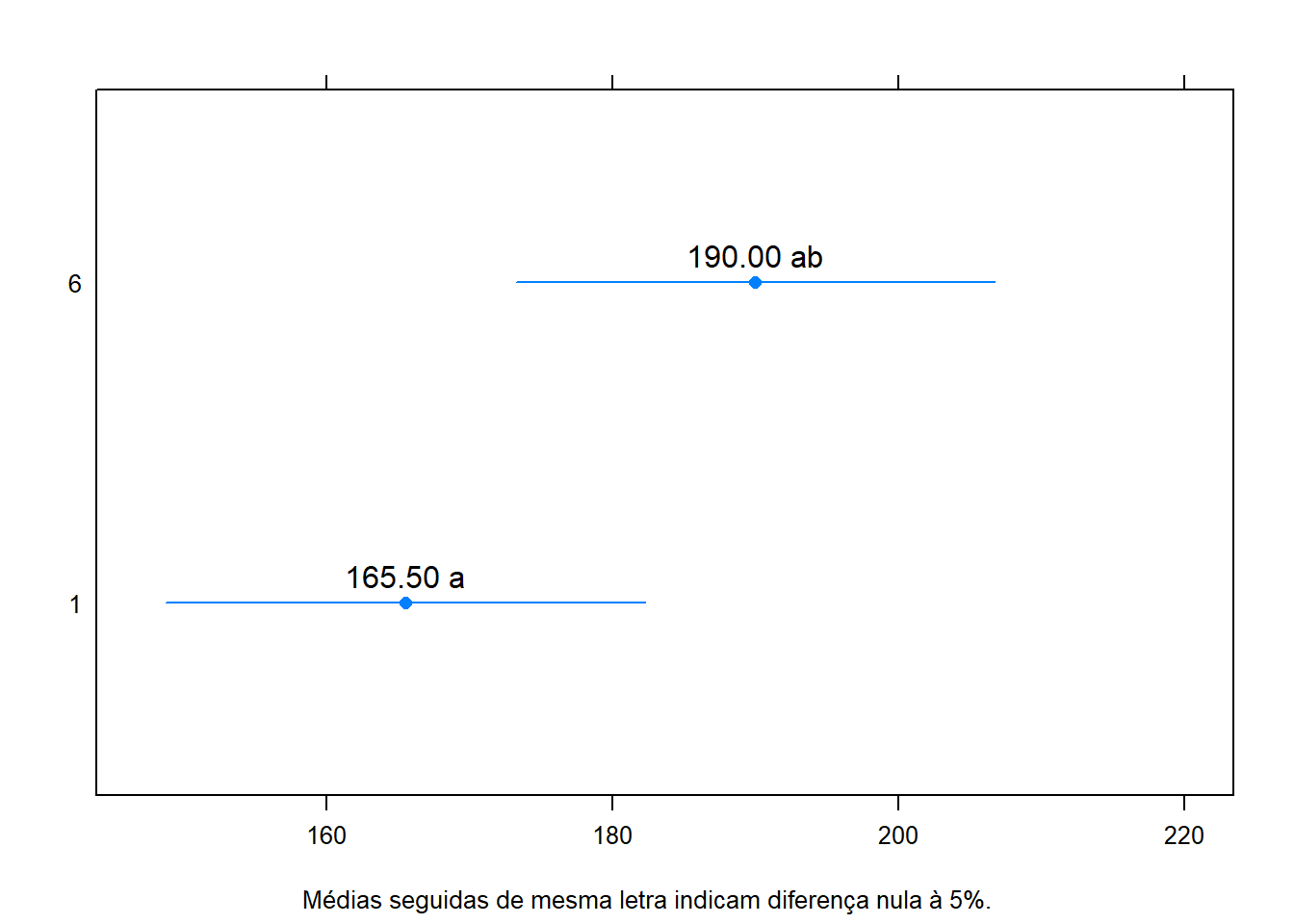

8.3.3 Exercicio para entregar

DiasEg9.4 help(“DiasEg9.4”)

BarbinPg104 help(“BarbinPg104”)

ZimmermannTb12.27 help(ZimmermannTb12.27)

ZimmermannTb12.26 help(ZimmermannTb12.26)

StorckEg2.3.5 help(StorckEg2.3.5)

ZimmermannTb16.10 help(ZimmermannTb16.10)

8.4 Regressão Linear simples

Iremos utilizar o pacote tidyverse:

library(tidyverse)

## -- Attaching packages ----------------------------------------- tidyverse 1.3.0 --

## v tibble  3.0.1     v purrr   0.3.4
## v tidyr   1.0.2     v stringr 1.4.0
## v readr   1.3.1     v forcats 0.5.0

## -- Conflicts -------------------------------------------- tidyverse_conflicts() --
## x dplyr::arrange()      masks plyr::arrange()
## x purrr::compact()      masks plyr::compact()
## x dplyr::count()        masks plyr::count()
## x tidyr::expand()       masks reshape::expand()
## x dplyr::failwith()     masks plyr::failwith()
## x dplyr::filter()       masks stats::filter()
## x dplyr::id()           masks plyr::id()
## x dplyr::lag()          masks stats::lag()
## x latticeExtra::layer() masks ggplot2::layer()
## x dplyr::mutate()       masks plyr::mutate()
## x reshape::rename()     masks dplyr::rename(), plyr::rename()
## x dplyr::select()       masks MASS::select()
## x dplyr::summarise()    masks plyr::summarise()
## x dplyr::summarize()    masks plyr::summarize()

Regressão linear é uma equação para estimar a condicional (valor esperado) de uma variável y, dados os valores de algumas outras variáveis x.

y= a+bx

Vamos utilizar o exemplo do banco de dados do R:

View(Orange)

qplot(x=age,y=circumference,data=Orange)

cor.test(Orange$age,Orange$circumference)

## 
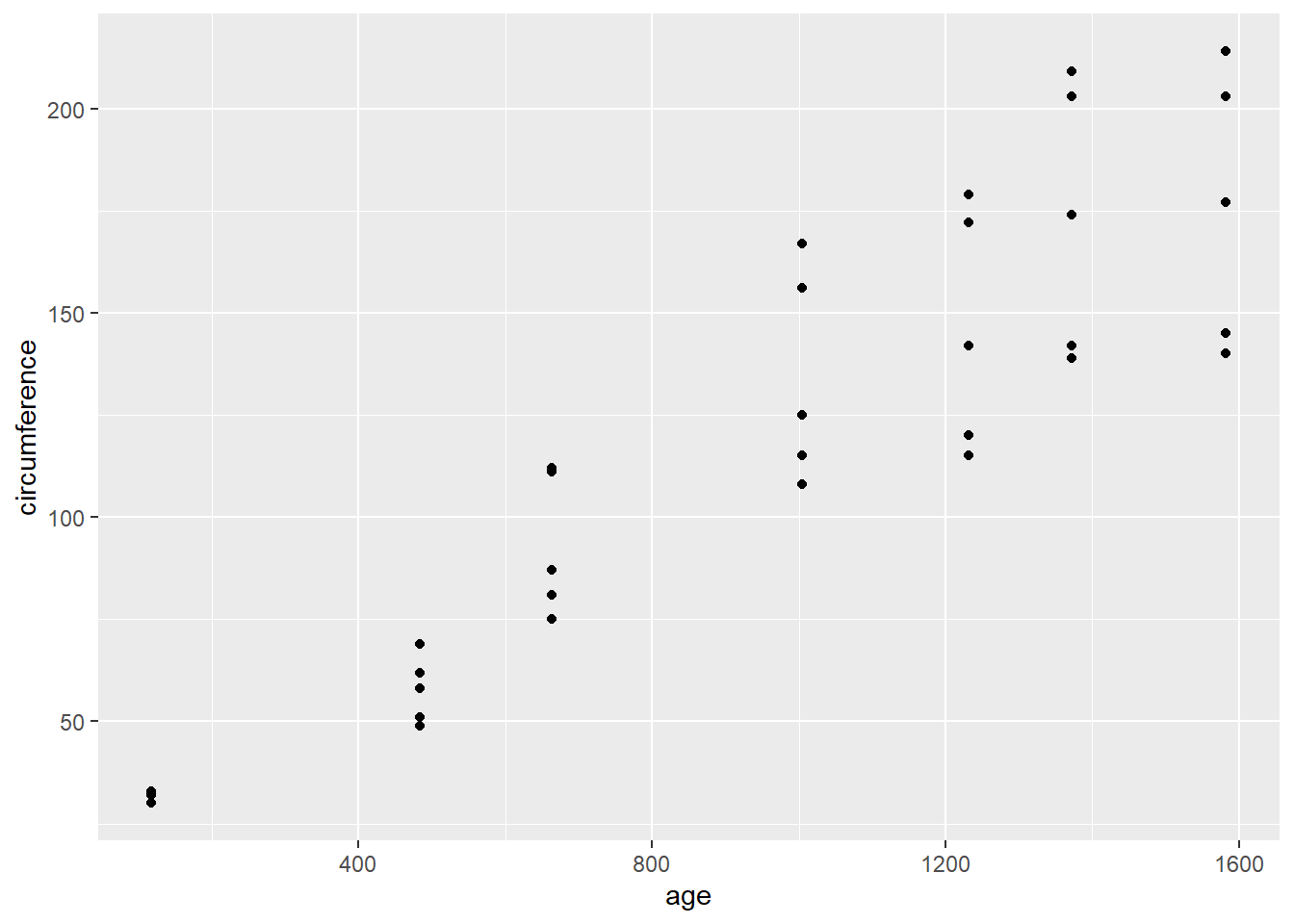
##  Pearson's product-moment correlation
## 
## data:  Orange$age and Orange$circumference
## t = 12.9, df = 33, p-value = 1.931e-14
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.8342364 0.9557955
## sample estimates:
##       cor 
## 0.9135189

rl<- lm(circumference ~ age , data = Orange)

Zerando o intercepto

rl0<- lm(circumference ~ 0+ age , data = Orange)

plot(rl) #plots diagnósticos

shapiro.test (residuals(rl))

## 
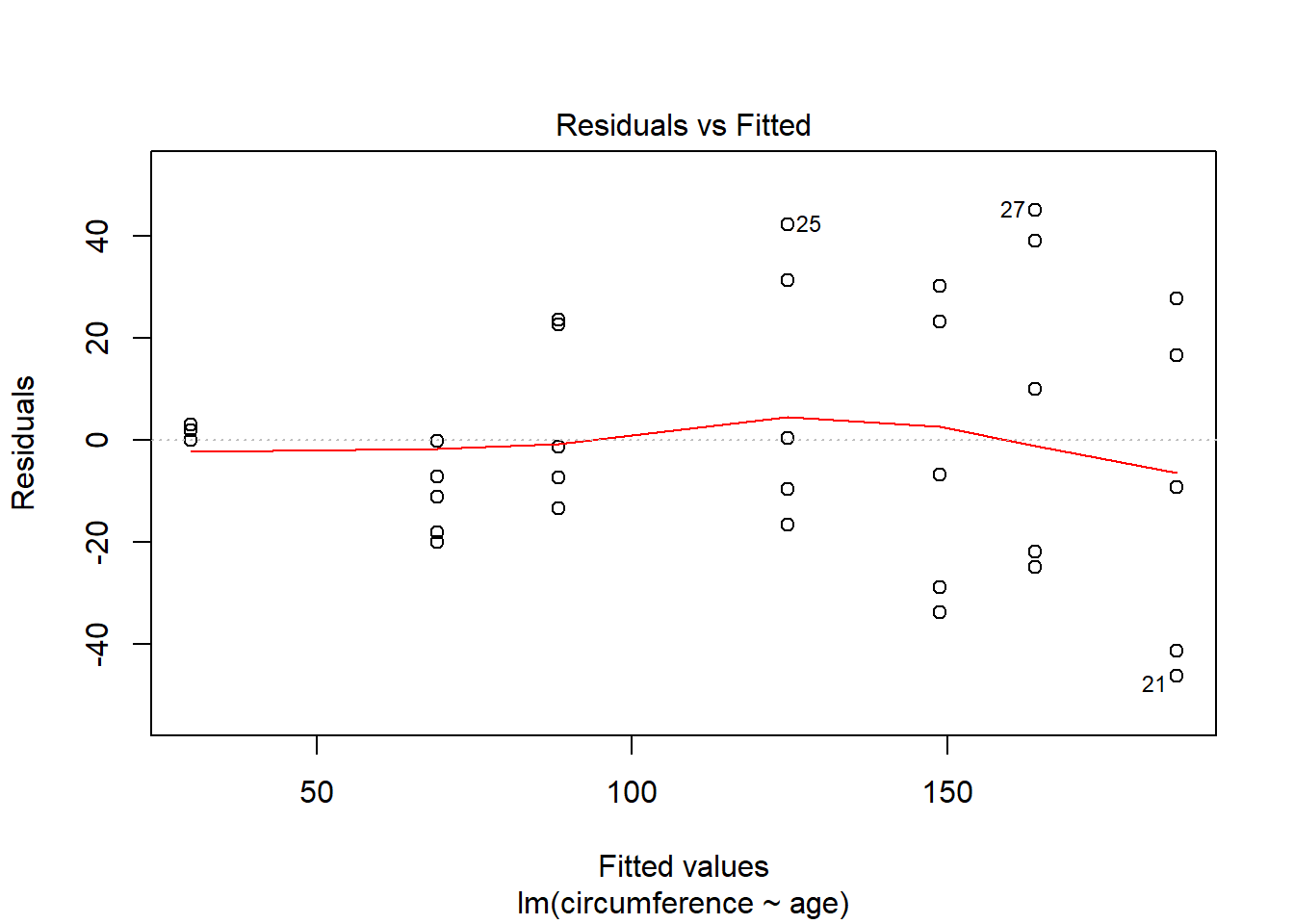
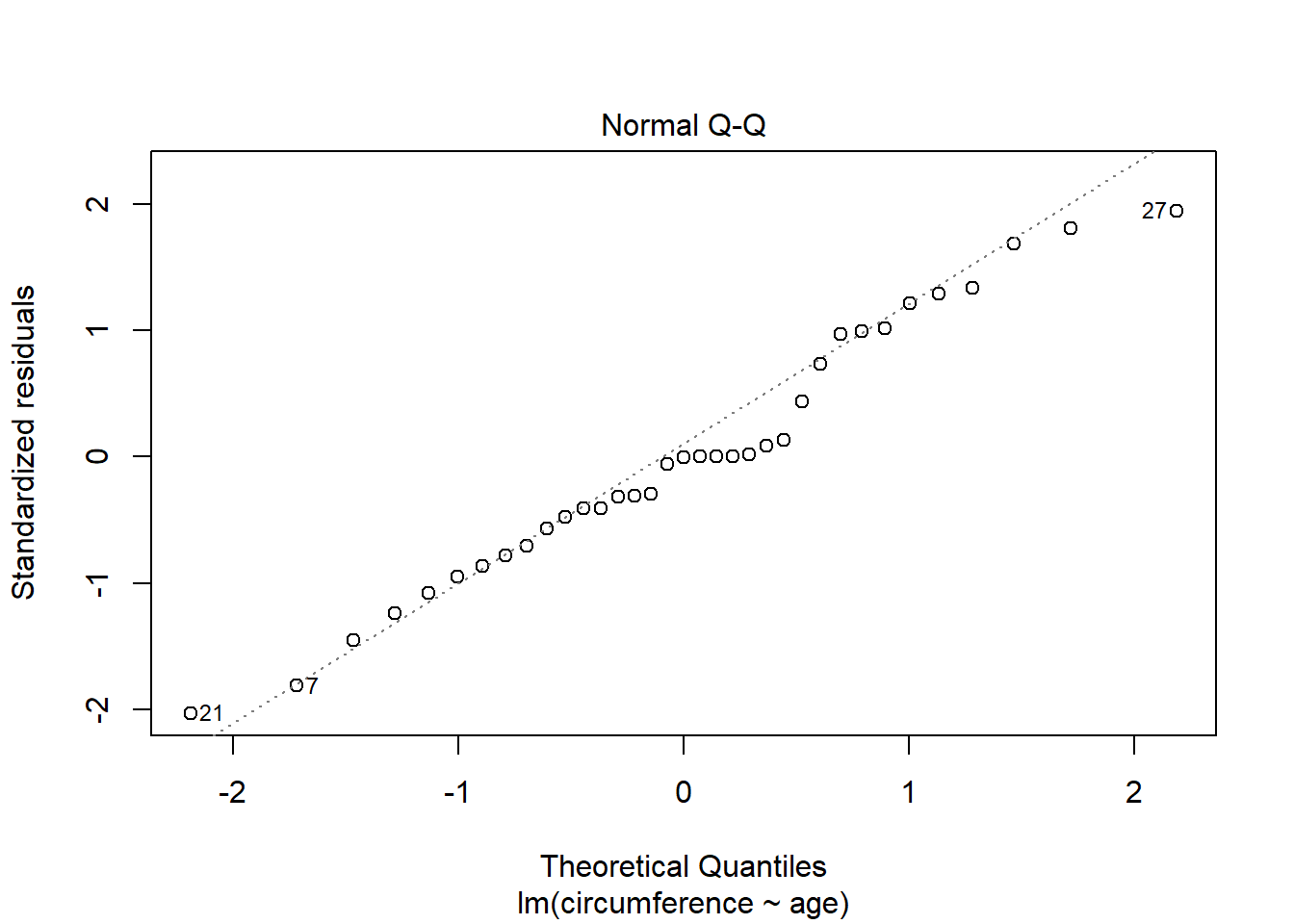
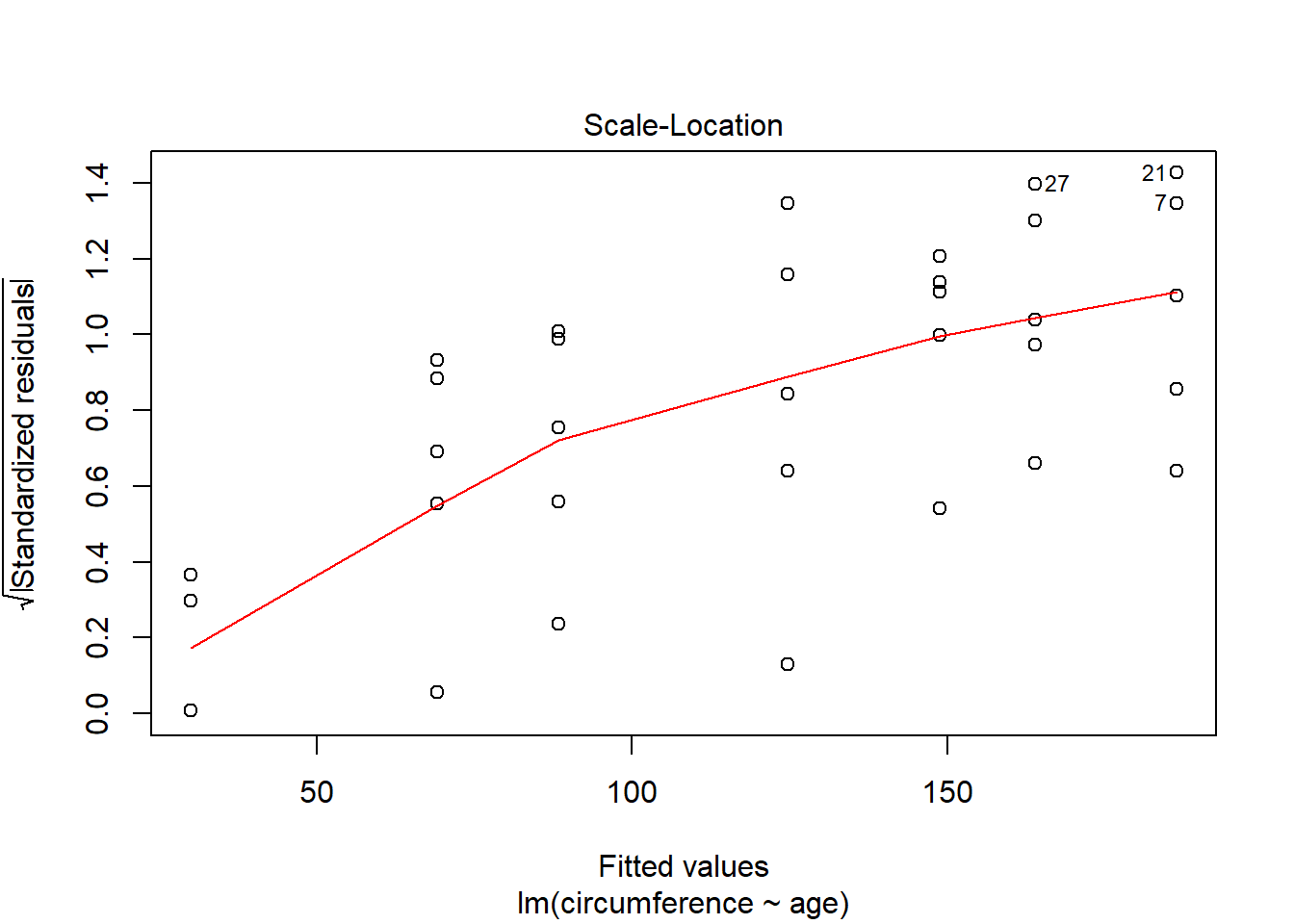
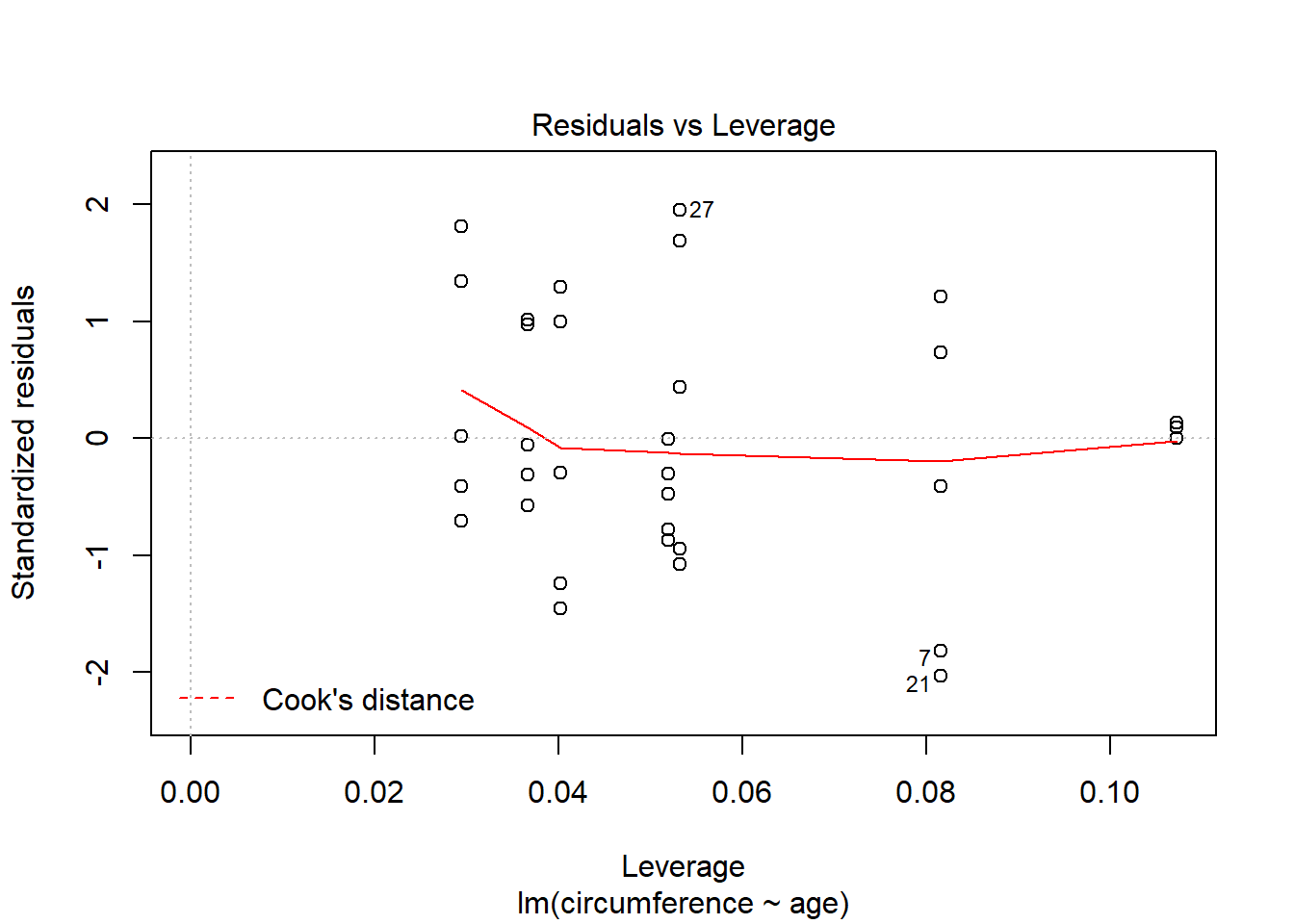
##  Shapiro-Wilk normality test
## 
## data:  residuals(rl)
## W = 0.97289, p-value = 0.5273

bartlett.test(rl$res, Orange$Tree, Orange$age)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  rl$res and Orange$Tree
## Bartlett's K-squared = 2.7663, df = 4, p-value = 0.5977

Resultado da Regressãolinear:

summary(rl)

## 
## Call:
## lm(formula = circumference ~ age, data = Orange)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -46.310 -14.946  -0.076  19.697  45.111 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 17.399650   8.622660   2.018   0.0518 .  
## age          0.106770   0.008277  12.900 1.93e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 23.74 on 33 degrees of freedom
## Multiple R-squared:  0.8345, Adjusted R-squared:  0.8295 
## F-statistic: 166.4 on 1 and 33 DF,  p-value: 1.931e-14

Rejeição da hipótese nula (variáveis não são relacionadas) valor p <0.005 R-square explica o quanto o modelo explica da variação

Gráfico:

ggplot(Orange,aes(x=age,y=circumference))+ geom_point(colour="steelblue",size=4)+
  geom_smooth(method="lm",colour="black")+labs(title="Regressão linear de Orange")+
  theme_minimal()

## `geom_smooth()` using formula 'y ~ x'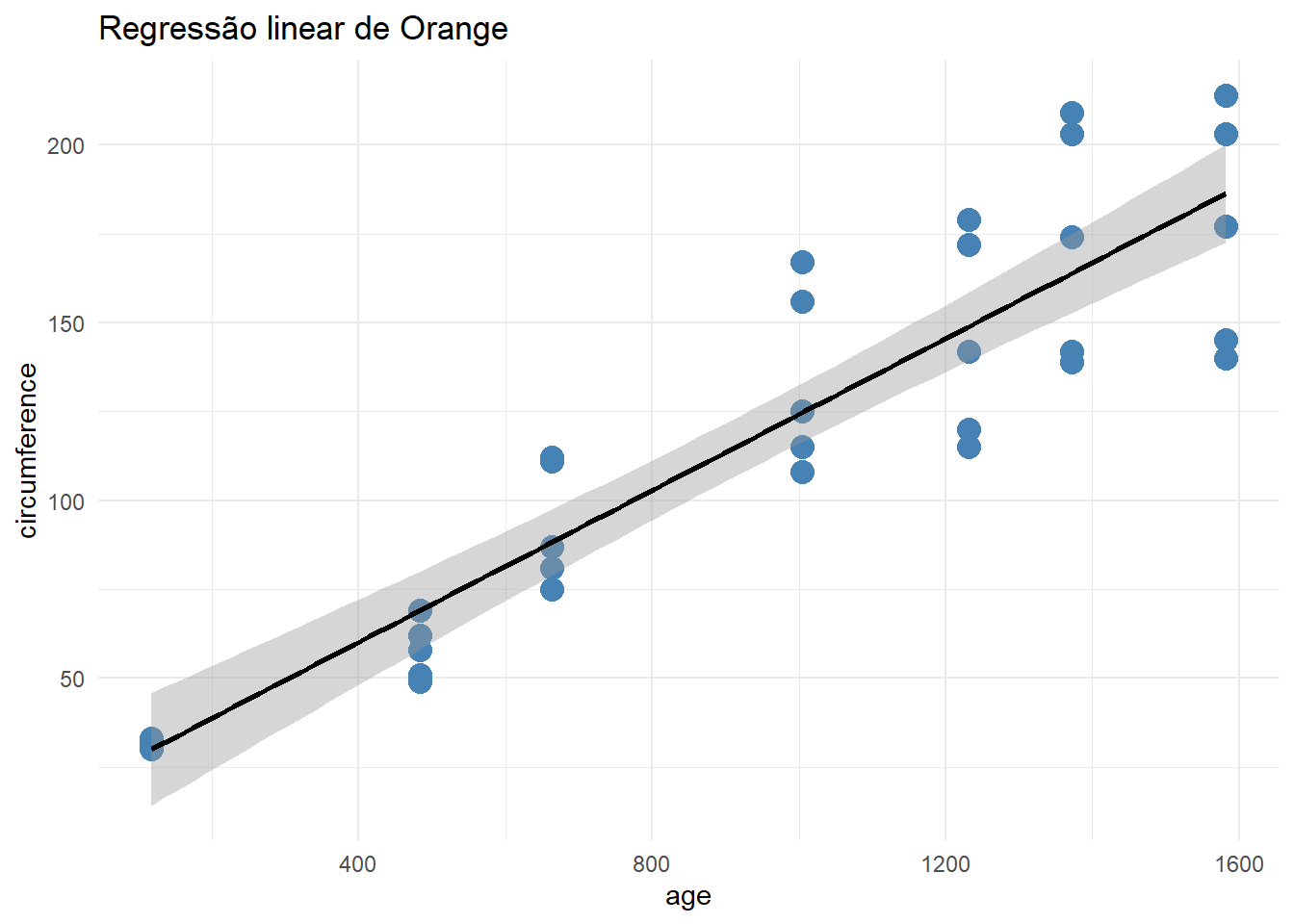

Gerar gráficos com o pacote ggpmisc:

library(ggpmisc)

Gráfico:

formula <- y ~ poly(x, 2, raw = TRUE)
ggplot(Orange, aes(x=age, y=circumference)) +
  geom_point() +
  geom_smooth(method = "lm", formula = formula) +
  stat_poly_eq(aes(label =  paste(..eq.label.., ..adj.rr.label.., sep = "~~~~")),
    formula = formula, parse = TRUE)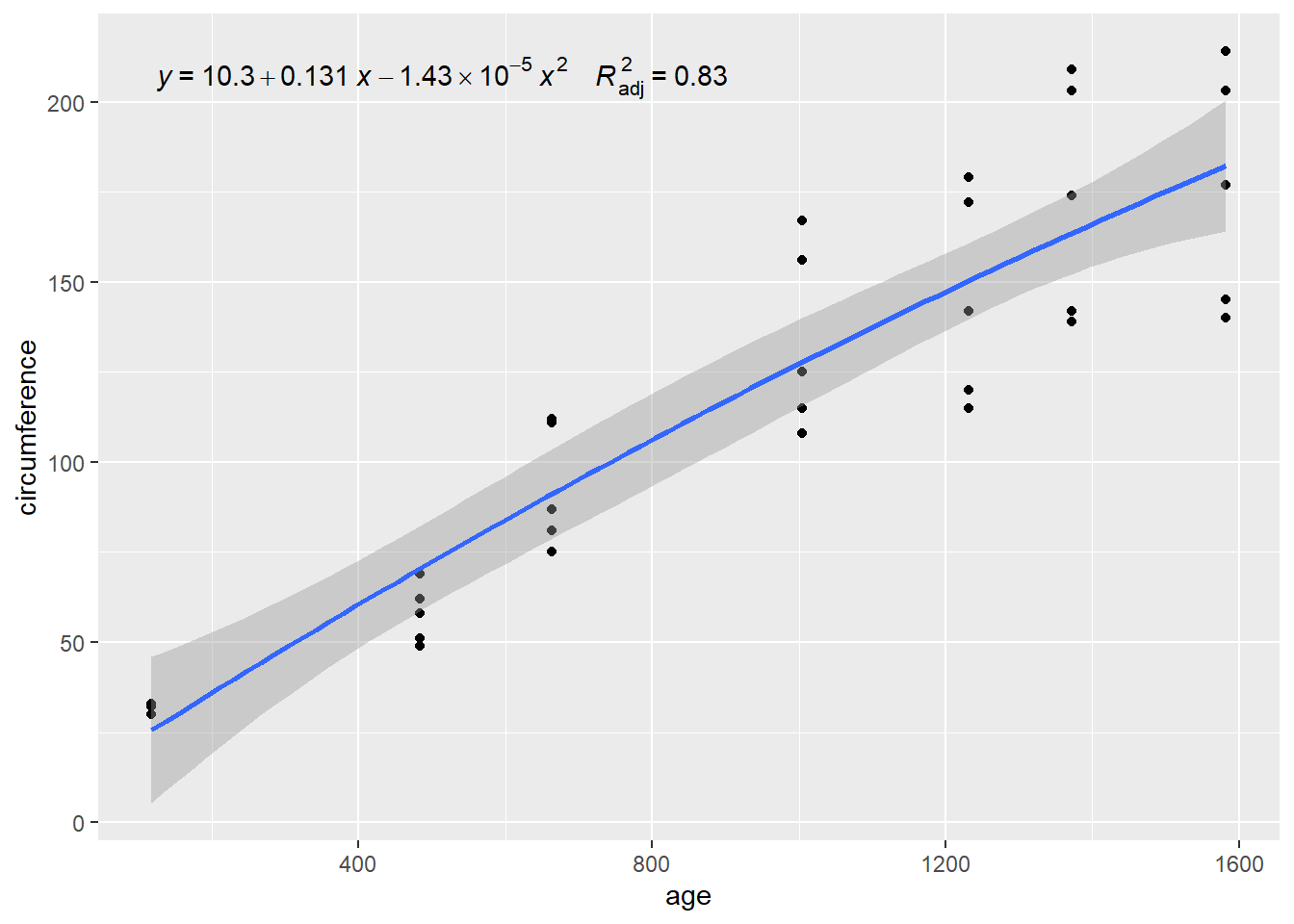

Outras funções interessantes:

coefficients(rl) # coeficientes do modelo

## (Intercept)         age 
##  17.3996502   0.1067703

confint(rl, level=0.95) # intervalo de confiança

##                   2.5 %     97.5 %
## (Intercept) -0.14328303 34.9425835
## age          0.08993141  0.1236092

fitted(rl) # valores previstos

##         1         2         3         4         5         6         7         8 
##  29.99855  69.07649  88.29515 124.59706 148.83392 163.88854 186.31030  29.99855 
##         9        10        11        12        13        14        15        16 
##  69.07649  88.29515 124.59706 148.83392 163.88854 186.31030  29.99855  69.07649 
##        17        18        19        20        21        22        23        24 
##  88.29515 124.59706 148.83392 163.88854 186.31030  29.99855  69.07649  88.29515 
##        25        26        27        28        29        30        31        32 
## 124.59706 148.83392 163.88854 186.31030  29.99855  69.07649  88.29515 124.59706 
##        33        34        35 
## 148.83392 163.88854 186.31030

residuals(rl) # residuais

##             1             2             3             4             5 
##   0.001451402 -11.076487573  -1.295146086  -9.597056609 -28.833920400 
##             6             7             8             9            10 
## -21.888536235 -41.310304499   3.001451402  -0.076487573  22.704853914 
##            11            12            13            14            15 
##  31.402943391  23.166079600  39.111463765  16.689695501   0.001451402 
##            16            17            18            19            20 
## -18.076487573 -13.295146086 -16.597056609 -33.833920400 -24.888536235 
##            21            22            23            24            25 
## -46.310304499   2.001451402  -7.076487573  23.704853914  42.402943391 
##            26            27            28            29            30 
##  30.166079600  45.111463765  27.689695501   0.001451402 -20.076487573 
##            31            32            33            34            35 
##  -7.295146086   0.402943391  -6.833920400  10.111463765  -9.310304499

anova(rl) # tabela ANOVA

## Analysis of Variance Table
## 
## Response: circumference
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## age        1  93772   93772  166.42 1.931e-14 ***
## Residuals 33  18595     563                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Qualquer modelo de regressão polinomial pode ser obtido com um comando simples: o lm() que vem do inglês “linear models”.

Veja o exemplo abaixo:

fert<-c(10,20,30,40,50,60,70,80,90,100)
prod<-c(42,61,81,94,98,96,83,79,59,43)
plot(fert,prod)

dados = data.frame(fert,prod)

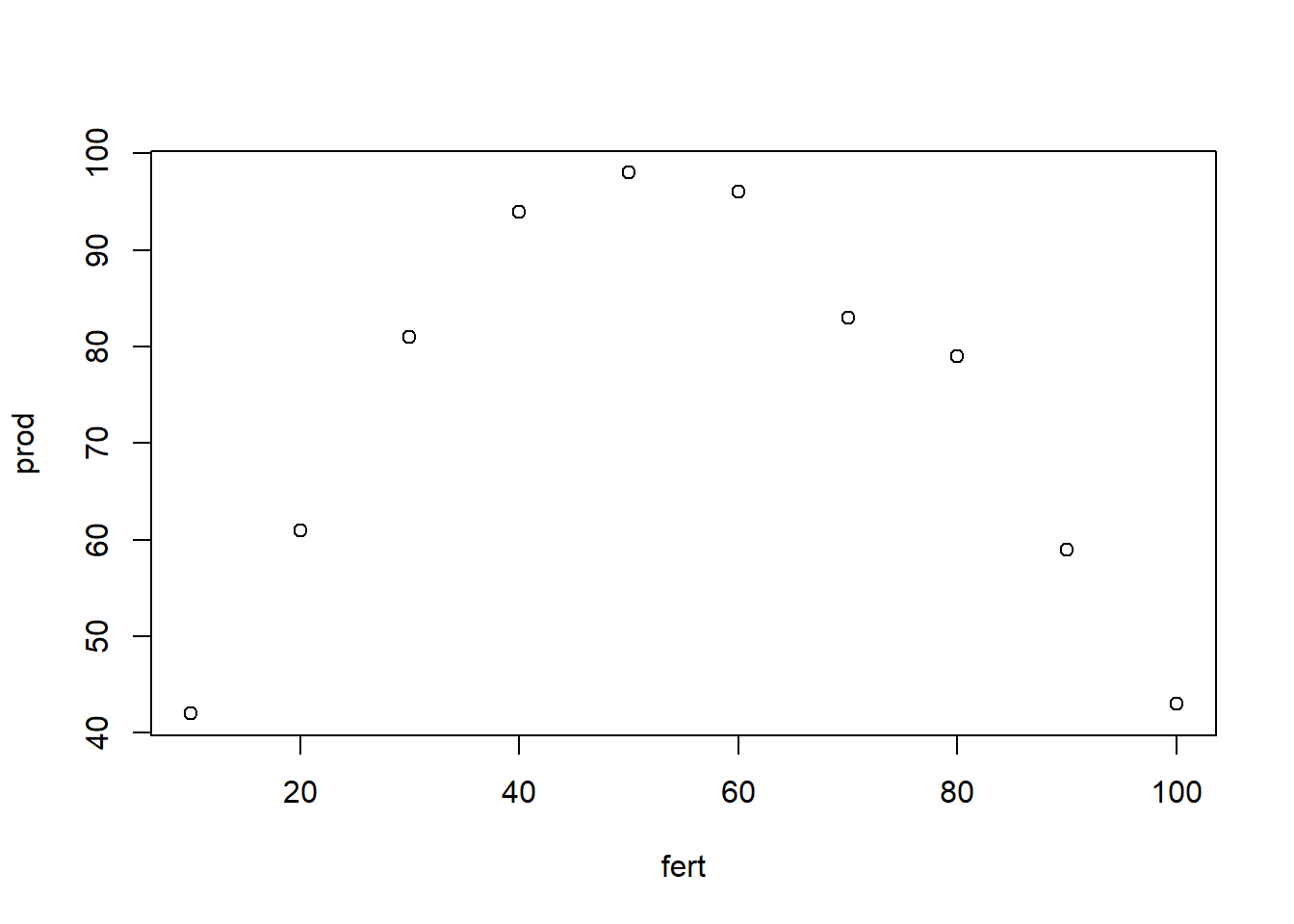
Observe a necessidade do argumento I() para interações como x^2:

reg <- lm ( #ajusta uma Regressão
        prod ~ fert + I (fert^2)) #modelo de Regressão quadrática
reg

## 
## Call:
## lm(formula = prod ~ fert + I(fert^2))
## 
## Coefficients:
## (Intercept)         fert    I(fert^2)  
##    15.51667      2.95720     -0.02716

Para “desenhar” a curva ajustada:

#curve(15.51667+2.95720*x-0.02716*x*x,0,100,add=T,col=2)

Várias outras análises podem ser feitas como anteriormente na regressão linear. Veja uma delas:

 anova(reg)

## Analysis of Variance Table
## 
## Response: prod
##           Df Sum Sq Mean Sq  F value    Pr(>F)    
## fert       1    7.6     7.6   0.5878    0.4683    
## I(fert^2)  1 3894.6  3894.6 302.2072 5.126e-07 ***
## Residuals  7   90.2    12.9                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

 formula <- y ~ poly(x, 2, raw = TRUE)
 ggplot(dados, aes(x=fert, y=prod)) +
   geom_point() +
   geom_smooth(method = "lm", formula = formula) +
   stat_poly_eq(aes(label =  paste(..eq.label.., ..adj.rr.label.., 
     sep = "~~italic(\"with\")~~")),
     formula = formula, parse = TRUE)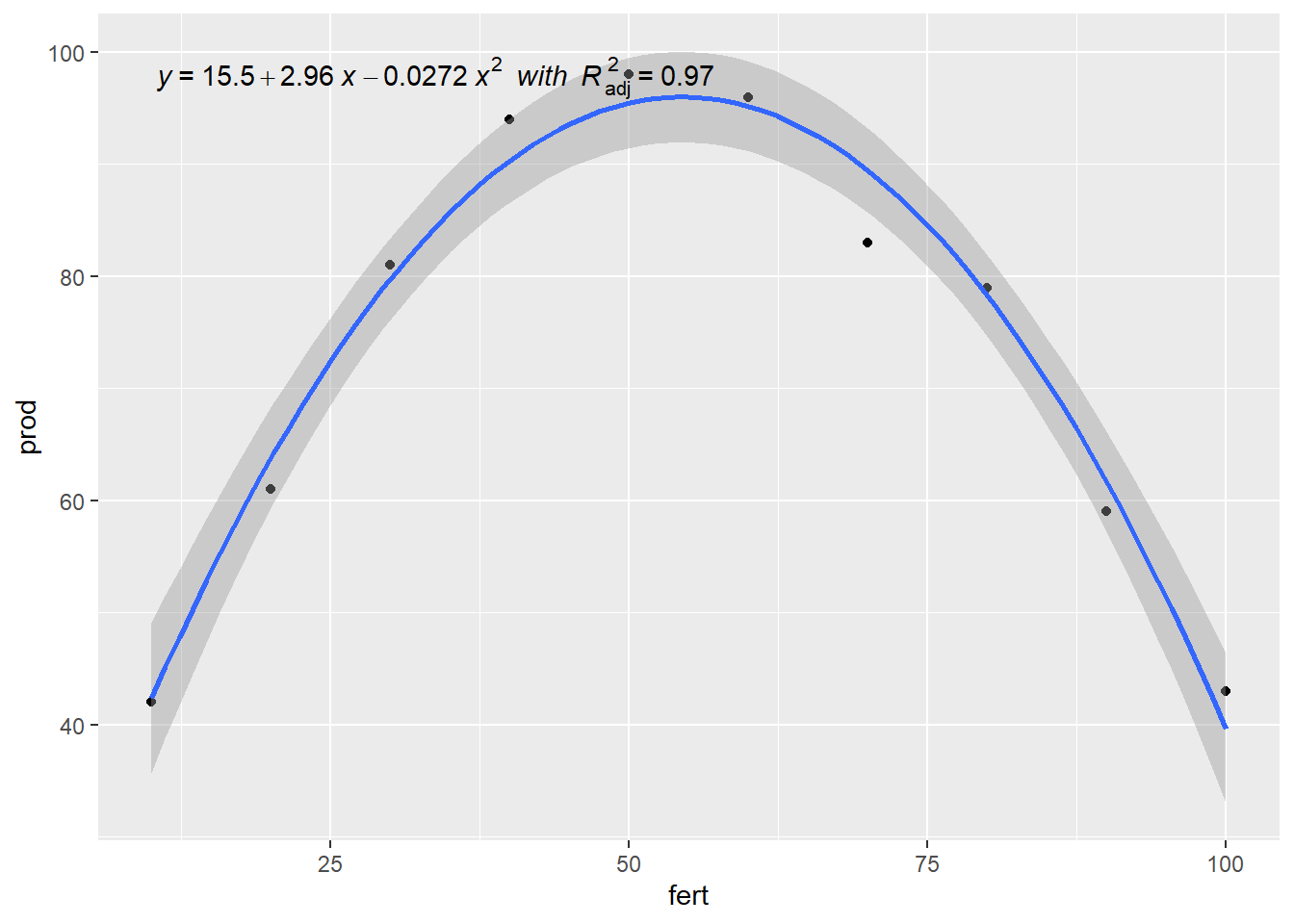

8.5 Regressão Linear Multipla

Os modelos múltiplos são aqueles em que duas ou mais variáveis independentes influenciam na variação da variável dependente. Eles podem ser de grau 1,2 ou maior. O exemplo a seguir aborda uma regressão polinomial multipla de 2º grau, com duas variáveis independentes.

y= a+ bx + b1x1 + b2x2 + b3x3…

Exemplo:

library(car)

## Loading required package: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:purrr':
## 
##     some

## The following object is masked from 'package:dplyr':
## 
##     recode

data(iris)
head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

VIF - variation inflation factor / fator de inflação da variância:

fit1<-lm(Sepal.Length ~ Sepal.Width + Petal.Length, data=iris)

vif(fit1)# ok, valores <5

##  Sepal.Width Petal.Length 
##     1.224831     1.224831

summary(fit1)

## 
## Call:
## lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.96159 -0.23489  0.00077  0.21453  0.78557 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   2.24914    0.24797    9.07 7.04e-16 ***
## Sepal.Width   0.59552    0.06933    8.59 1.16e-14 ***
## Petal.Length  0.47192    0.01712   27.57  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3333 on 147 degrees of freedom
## Multiple R-squared:  0.8402, Adjusted R-squared:  0.838 
## F-statistic: 386.4 on 2 and 147 DF,  p-value: < 2.2e-16

fit2 <- lm (Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width, data=iris)
vif(fit2) #problemático, valores>10

##  Sepal.Width Petal.Length  Petal.Width 
##     1.270815    15.097572    14.234335

summary(fit2)

## 
## Call:
## lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width, 
##     data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.82816 -0.21989  0.01875  0.19709  0.84570 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.85600    0.25078   7.401 9.85e-12 ***
## Sepal.Width   0.65084    0.06665   9.765  < 2e-16 ***
## Petal.Length  0.70913    0.05672  12.502  < 2e-16 ***
## Petal.Width  -0.55648    0.12755  -4.363 2.41e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3145 on 146 degrees of freedom
## Multiple R-squared:  0.8586, Adjusted R-squared:  0.8557 
## F-statistic: 295.5 on 3 and 146 DF,  p-value: < 2.2e-16

fit3<-lm(Sepal.Length ~ Sepal.Width * Petal.Length, data=iris)
vif(fit3)# muito problemático, valores muito altos

##              Sepal.Width             Petal.Length Sepal.Width:Petal.Length 
##                 6.457248                81.811109                69.223186

summary(fit3)

## 
## Call:
## lm(formula = Sepal.Length ~ Sepal.Width * Petal.Length, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.99594 -0.21165 -0.01652  0.21244  0.77249 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               1.40438    0.53253   2.637  0.00926 ** 
## Sepal.Width               0.84996    0.15800   5.379 2.91e-07 ***
## Petal.Length              0.71846    0.13886   5.174 7.45e-07 ***
## Sepal.Width:Petal.Length -0.07701    0.04305  -1.789  0.07571 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3308 on 146 degrees of freedom
## Multiple R-squared:  0.8436, Adjusted R-squared:  0.8404 
## F-statistic: 262.5 on 3 and 146 DF,  p-value: < 2.2e-16

Outras funções interessantes:

coefficients(fit1) # coeficientes

##  (Intercept)  Sepal.Width Petal.Length 
##    2.2491402    0.5955247    0.4719200

confint(fit1, level=0.95) # Intervalos de confiança

##                  2.5 %    97.5 %
## (Intercept)  1.7590943 2.7391860
## Sepal.Width  0.4585161 0.7325334
## Petal.Length 0.4380915 0.5057486

fitted(fit1) # valores previstos

##        1        2        3        4        5        6        7        8 
## 4.994165 4.696402 4.768315 4.803147 5.053717 5.373951 4.934612 4.981804 
##        9       10       11       12       13       14       15       16 
## 4.636850 4.803147 5.160462 5.028996 4.696402 4.554826 5.197543 5.577329 
##       17       18       19       20       21       22       23       24 
## 5.185183 4.994165 5.314398 5.220014 5.076188 5.160462 4.864949 5.016636 
##       25       26       27       28       29       30       31       32 
## 5.170572 4.790786 5.028996 5.041357 4.934612 4.909891 4.850339 4.981804 
##       33       34       35       36       37       38       39       40 
## 5.398672 5.411032 4.803147 4.721123 4.946973 5.053717 4.649210 4.981804 
##       41       42       43       44       45       46       47       48 
## 4.946973 4.232343 4.768315 5.088549 5.408782 4.696402 5.267206 4.815507 
##       49       50       51       52       53       54       55       56 
## 5.160462 4.875060 6.372844 6.278460 6.407675 5.506527 6.087442 6.040250 
##       57       58       59       60       61       62       63       64 
## 6.432396 5.235736 6.146994 5.697545 5.091910 6.017779 5.446975 6.194186 
##       65       66       67       68       69       70       71       72 
## 5.675074 6.171715 6.159355 5.791929 5.682935 5.578440 6.420036 5.804290 
##       73       74       75       76       77       78       79       80 
## 6.050360 6.134634 6.005418 6.112163 6.181826 6.395315 6.099802 5.449225 
##       81       82       83       84       85       86       87       88 
## 5.471696 5.424504 5.697545 6.263849 6.159355 6.397564 6.313291 5.695295 
##       89       90       91       92       93       94       95       96 
## 5.970587 5.625632 5.873953 6.206547 5.685185 5.176183 5.839121 6.017779 
##       97       98       99      100      101      102      103      104 
## 5.958226 6.005418 5.153712 5.851482 7.045892 6.263849 6.820043 6.618914 
##      105      106      107      108      109      110      111      112 
## 6.772851 7.150387 5.861592 6.949258 6.475088 7.271741 6.561612 6.358233 
##      113      114      115      116      117      118      119      120 
## 6.631275 6.097552 6.323402 6.655996 6.631275 7.673998 7.053753 5.918895 
##      121      122      123      124      125      126      127      128 
## 6.844764 6.229018 7.078474 6.169465 6.904316 6.986340 6.181826 6.348123 
##      129      130      131      132      133      134      135      136 
## 6.559362 6.772851 6.795322 7.532422 6.559362 6.323402 6.440257 6.914427 
##      137      138      139      140      141      142      143      144 
## 6.916677 6.690827 6.300931 6.643635 6.738019 6.502059 6.263849 6.939148 
##      145      146      147      148      149      150 
## 6.904316 6.489699 6.097552 6.489699 6.822293 6.442507

residuals(fit1) # residuais

##            1            2            3            4            5            6 
##  0.105835164  0.203597538 -0.068315407 -0.203146940 -0.053717311  0.026049253 
##            7            8            9           10           11           12 
## -0.334612361  0.018195635 -0.236849987  0.096853060  0.239538210 -0.228996369 
##           13           14           15           16           17           18 
##  0.103597538 -0.254826450  0.602456797  0.122670886  0.214817268  0.105835164 
##           19           20           21           22           23           24 
##  0.385601728 -0.120014265  0.323811627 -0.060461790 -0.264949295  0.083364102 
##           25           26           27           28           29           30 
## -0.370572381  0.209213530 -0.028996369  0.158643160  0.265387639 -0.209891419 
##           31           32           33           34           35           36 
## -0.050338944  0.418195635 -0.198671689  0.088967840  0.096853060  0.278876596 
##           37           38           39           40           41           42 
##  0.553027168 -0.153717311 -0.249210458  0.118195635  0.053027168  0.267656866 
##           43           44           45           46           47           48 
## -0.368315407 -0.088548844 -0.308782280  0.103597538 -0.167206269 -0.215507411 
##           49           50           51           52           53           54 
##  0.139538210  0.124940114  0.627156459  0.121540467  0.492324926 -0.006527240 
##           55           56           57           58           59           60 
##  0.412558362 -0.340249634 -0.132396016 -0.335735687  0.453005887 -0.497545135 
##           61           62           63           64           65           66 
## -0.091909796 -0.117778572  0.553025235 -0.094186117 -0.075074073  0.528284945 
##           67           68           69           70           71           72 
## -0.559354584  0.008070857  0.517065215  0.021559814 -0.520035545  0.295710386 
##           73           74           75           76           77           78 
##  0.249639775 -0.034633642  0.394581899  0.487837420  0.618174354  0.304685397 
##           79           80           81           82           83           84 
## -0.099802109  0.250775355  0.028304293  0.075496297  0.102454865 -0.263849183 
##           85           86           87           88           89           90 
## -0.759354584 -0.397564483  0.386708934  0.604704744 -0.370586568 -0.125632190 
##           91           92           93           94           95           96 
## -0.373952680 -0.106546588  0.114815336 -0.176183212 -0.239121147 -0.317778572 
##           97           98           99          100          101          102 
## -0.258226097  0.194581899 -0.053712150 -0.151481618 -0.745892067 -0.463849183 
##          103          104          105          106          107          108 
##  0.279957361 -0.318914152 -0.272850635  0.449613334 -0.961592209  0.350741820 
##          109          110          111          112          113          114 
##  0.224911740 -0.071741496 -0.061611557  0.041766810  0.168725377 -0.397552229 
##          115          116          117          118          119          120 
## -0.523401657 -0.255995565 -0.131274623  0.026001531  0.646247222  0.081105196 
##          121          122          123          124          125          126 
##  0.055236419 -0.629017650  0.621526280  0.130534825 -0.204316055  0.213660408 
##          127          128          129          130          131          132 
##  0.018174354 -0.248122599 -0.159361677  0.427149365  0.604678303  0.367577543 
##          133          134          135          136          137          138 
## -0.159361677 -0.023401657 -0.340256727  0.785573353 -0.616676526 -0.290827098 
##          139          140          141          142          143          144 
## -0.300930595  0.256364906 -0.038019102  0.397940918 -0.463849183 -0.139147588 
##          145          146          147          148          149          150 
## -0.204316055  0.210301389  0.202447771  0.010301389 -0.622292518 -0.542506607

anova(fit1) # tabela anova

## Analysis of Variance Table
## 
## Response: Sepal.Length
##               Df Sum Sq Mean Sq F value    Pr(>F)    
## Sepal.Width    1  1.412   1.412  12.714 0.0004902 ***
## Petal.Length   1 84.427  84.427 760.059 < 2.2e-16 ***
## Residuals    147 16.329   0.111                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

vcov(fit1) # matriz de covariancia

##               (Intercept)   Sepal.Width  Petal.Length
## (Intercept)   0.061488936 -0.0166054883 -0.0026556385
## Sepal.Width  -0.016605488  0.0048063941  0.0005084458
## Petal.Length -0.002655638  0.0005084458  0.0002930149

8.5.1 Referência

MELO, M. P.; PETERNELI, L. A. Conhecendo o R: Um visão mais que estatística. Viçosa, MG: UFV, 2013. 222p. Cap. 1.

ZEVIANI, W. M. Estatástica Básica e Experimentação no R. 45p.

http://www.leg.ufpr.br/~paulojus/

https://docs.r4photobiology.info/ggpmisc/articles/user-guide-1.html

8.6 Regressão não linear

Para o ajuste de regressões não-lineares com o R, aconselhamos o uso da função nls() (modelo, dados e valores iniciais estimados dos parâmetros)

Exemplo:

Num projeto de construção de uma barragem é de grande interesse equacionar a relação entre a cota do nível d’água e o volume armazenado quando esta cota é atingida. Essa relação é obtida a partir de um diagrama cota-volume estimado através do levantamento topográfico da região onde será construída a barragem e suas respectivas curvas de nível. Suponha os dados a seguir, com a cota dada em metros e o volume em quilômetros cúbicos:

cota<-c(1,2,3,4,5,6,7,8,9,10) 
volume<-c(7,10,14,20,31,40,58,84,113,165) 
dados<-data.frame(cota,volume) 
plot(dados)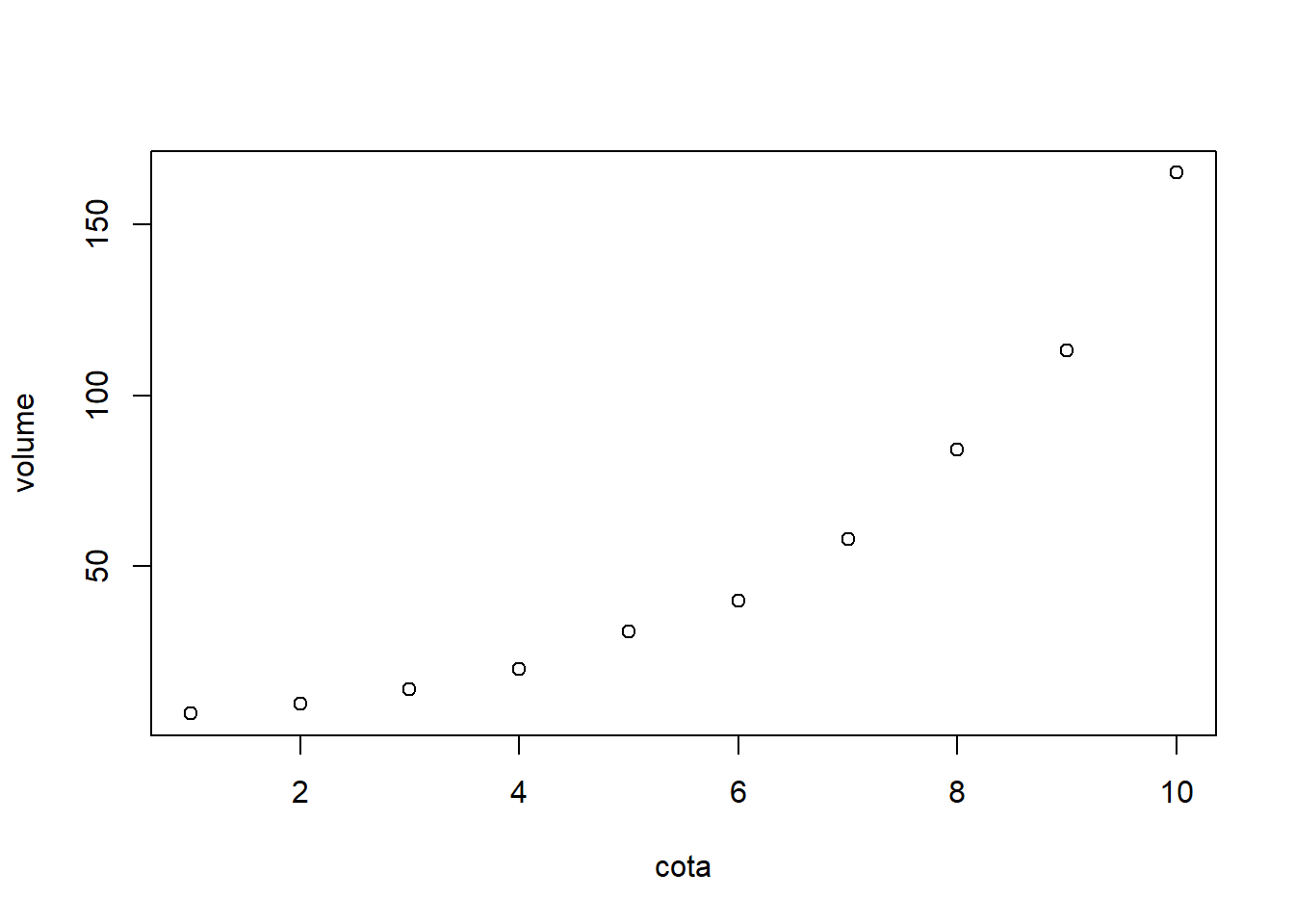

funcao <- volume~a*exp(b*cota) 
exponencial <- nls(funcao, #modelo que se deseja ajustar($) 
    dados, #data.frame com o conjunto de dados
    start=c(a=1,b=1)) #valores iniciais dos parâmetros($$)   
    summary(exponencial)

## 
## Formula: volume ~ a * exp(b * cota)
## 
## Parameters:
##   Estimate Std. Error t value Pr(>|t|)    
## a 5.116389   0.227553   22.48 1.62e-08 ***
## b 0.346720   0.004879   71.06 1.71e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.559 on 8 degrees of freedom
## 
## Number of iterations to convergence: 14 
## Achieved convergence tolerance: 2.694e-07

Desenhando a curva ajustada:

plot(dados) 
curve(5.1163887*exp(0.34672*x), 1, #limite inferior eixo das abscissas
      10, #limite superior
      add=T, #acrescentar no gráfico anterior 
      col=2) #cor da curva (2 = vermelha)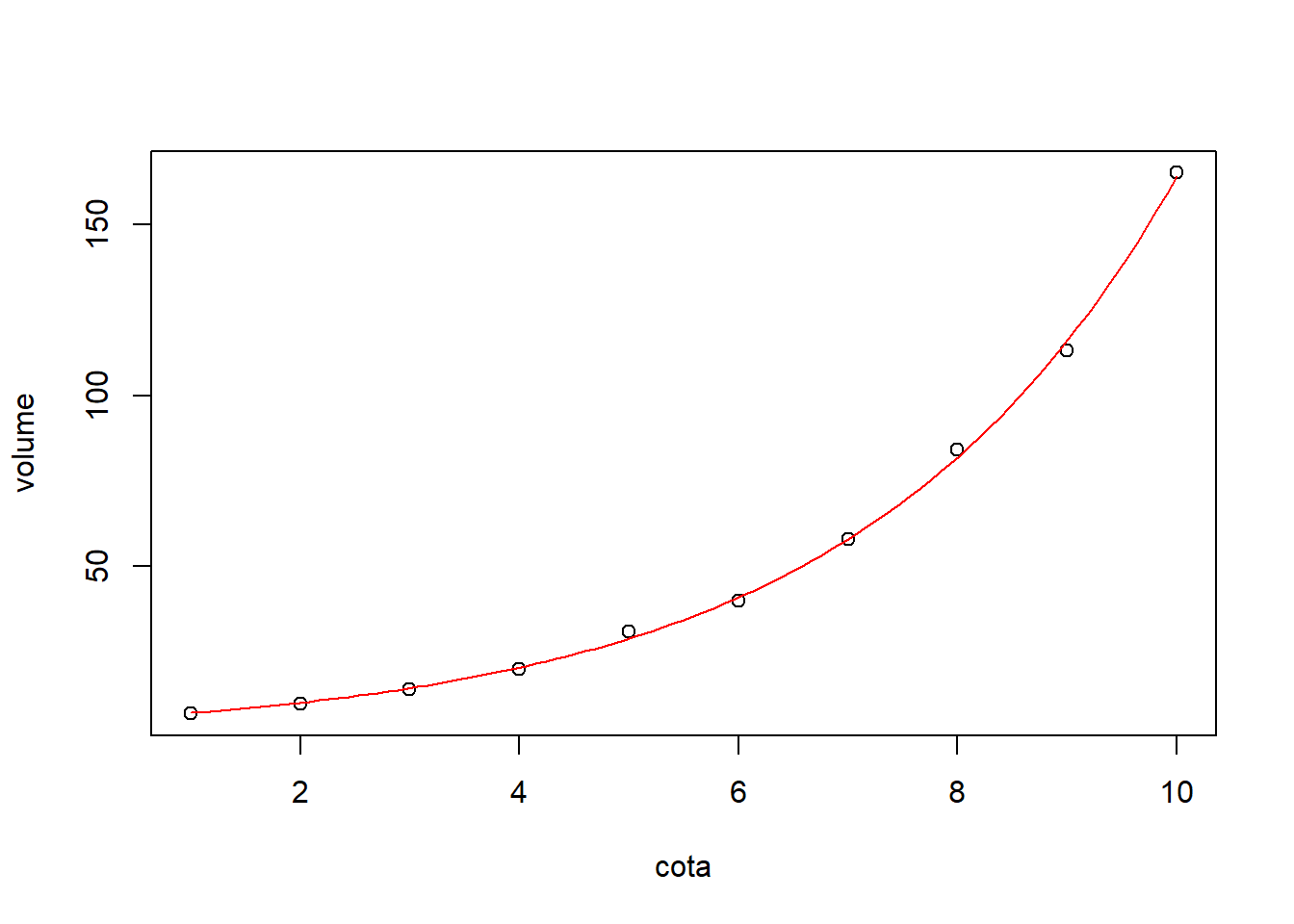

8.6.1 Curva de retenção de água no solo

O objetivo é determinar da curva de retenção de água no solo estimada segundo modelo de van Genutchen para cada uma das amostras.

Fonte: http://www.leg.ufpr.br/~paulojus/embrapa/

cra <- read.table("http://www.leg.ufpr.br/~paulojus/dados/cra.csv", head = T, sep = ",") 
head(cra)

##   am pot      u
## 1 30  10 0.3071
## 2 30  19 0.2931
## 3 30  30 0.2828
## 4 30  45 0.2753
## 5 30  63 0.2681
## 6 30  64 0.2628

cra <- transform(cra, am = as.factor(am)) 
summary(cra)

##   am          pot                u         
##  30:15   Min.   :   10.0   Min.   :0.0636  
##  41:13   1st Qu.:   58.5   1st Qu.:0.1199  
##          Median :  107.5   Median :0.1969  
##          Mean   : 2139.8   Mean   :0.1879  
##          3rd Qu.: 1550.0   3rd Qu.:0.2436  
##          Max.   :26300.0   Max.   :0.3071

Isolar a amostra 30:

cra30 <- subset(cra, am == "41")
cra30

##    am   pot      u
## 16 41    11 0.2407
## 17 41    14 0.2209
## 18 41    34 0.2100
## 19 41    65 0.2004
## 20 41    94 0.1935
## 21 41   110 0.1842
## 22 41   157 0.1706
## 23 41  1700 0.1023
## 24 41  1200 0.1180
## 25 41  1100 0.1261
## 26 41  1500 0.1101
## 27 41  2300 0.0917
## 28 41 12100 0.0636

Figura com o eixo horizontal com logarítmo (base 10), dados de umidade versus pressão aplicada na amostra:

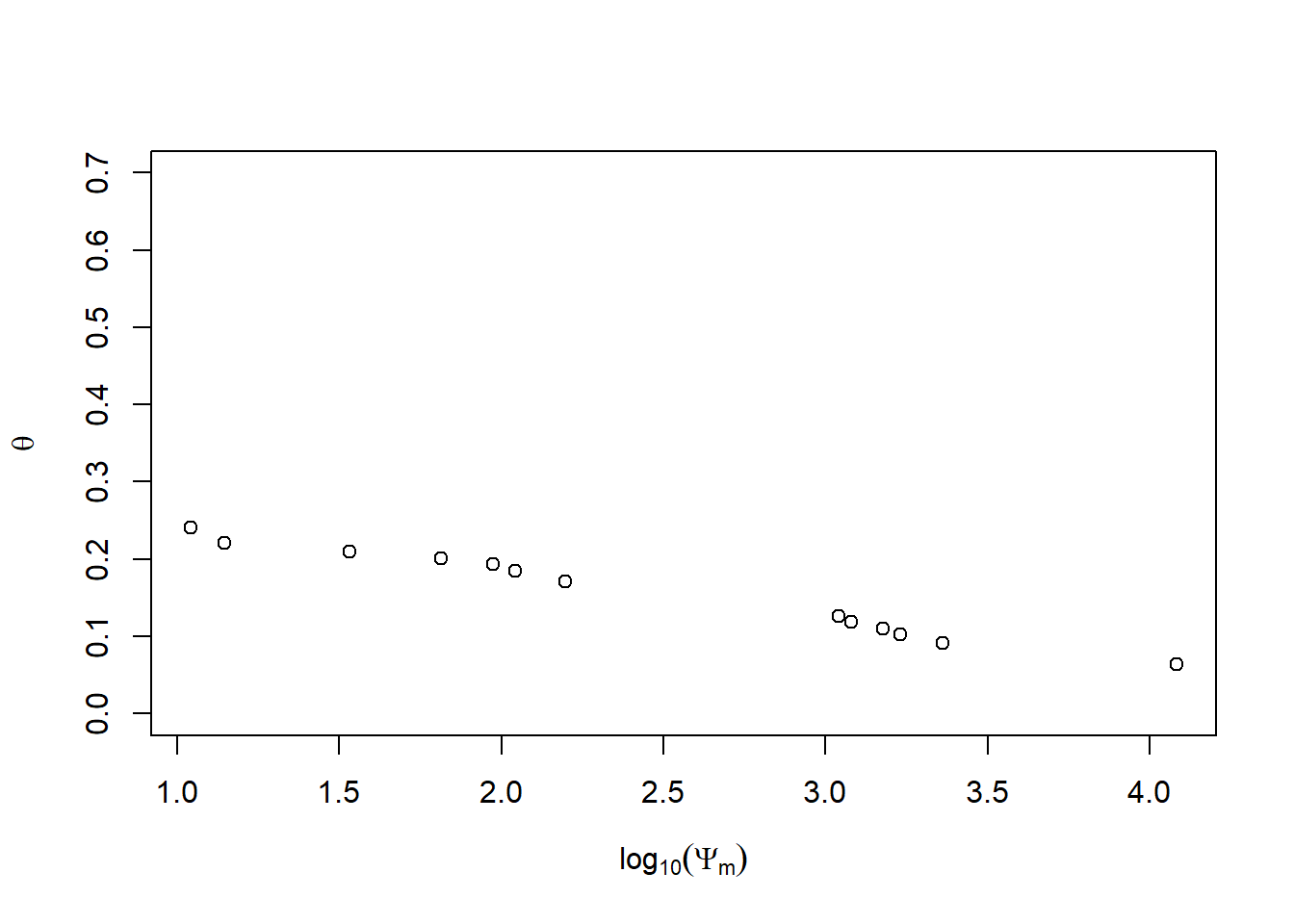
with(cra30, plot(u ~ log10(pot), xlab = expression(log[10](Psi[m])), ylab = expression(theta), ylim = c(0, 0.7)))

Figura dos dados de umidade versus pressão aplicada na amostra:

with(cra30, plot(u ~ pot, xlab = expression(Psi[m]), 
                 ylab = expression(theta),
                 ylim = c(0,0.7))) 
        curve(0.05 + (0.35 - 0.05)/((1 + (0.1 * x)^1.3)^(1 - 1/1.3)), from = 0, 
  to = 27000, add = T, lty = 2)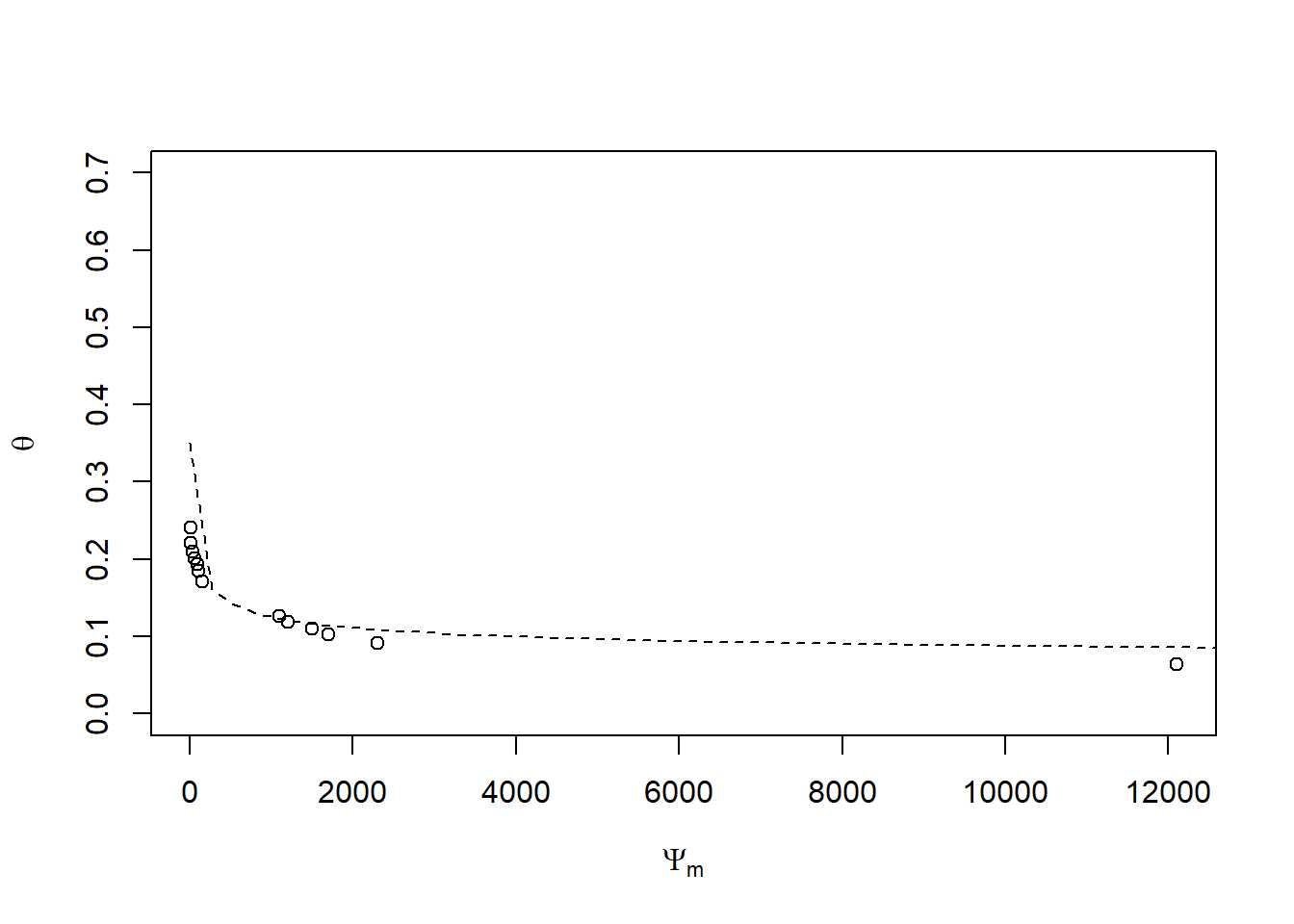

Definidos os valores iniciais prossegue-se com o ajuste do modelo conforme os comandos a seguir:

fit30 = nls(u ~ ur + (us - ur)/((1 + (alpha * pot)^n)^(1 - 1/n)), data = cra30, start = list(us = 0.35, ur = 0.05, alpha = 0.1, n = 1.3))

summary(fit30)

## 
## Formula: u ~ ur + (us - ur)/((1 + (alpha * pot)^n)^(1 - 1/n))
## 
## Parameters:
##        Estimate Std. Error t value Pr(>|t|)    
## us     0.243148   0.009446  25.741 9.71e-10 ***
## ur    -0.122402   0.171614  -0.713    0.494    
## alpha  0.035928   0.022324   1.609    0.142    
## n      1.113320   0.079473  14.009 2.04e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.006207 on 9 degrees of freedom
## 
## Number of iterations to convergence: 9 
## Achieved convergence tolerance: 9.545e-06